Utilisez des archives de données pour stocker des séries temporelles

Les heures d'arrivée dans un PoissonProcess sont indépendants et suivent un ExponentialDistribution. Vous pouvez simuler le trajet d'un PoissonProcess en envoyant des signaux à une Databin dans des intervalles de temps spécifiés par la simulation d'une loi exponentielle.

In[1]:=

SeedRandom["11"]; \[Lambda] = 0.5; times = RandomVariate[ExponentialDistribution[\[Lambda]], 30];

Créez une Databin.

In[2]:=

bin = CreateDatabin[]

Out[2]=

Utilisez les temps simulés pour envoyer 1 aux archives de données dans des intervalles de temps.

In[3]:=

Table[DatabinAdd[bin, <|"arrivals" -> 1|>]; Pause[t], {t, times}];

Le signal enregistré avec des horodatages.

In[4]:=

TimeSeries[bin]

Out[4]=

Extrayez l'objet TimeSeries.

In[5]:=

ts1 = TimeSeries[bin]["arrivals"]

Out[5]=

Cette série temporelle est irrégulièrement échantillonnée.

In[6]:=

RegularlySampledQ[ts1]

Out[6]=

Supposons la TemporalRegularity pour qu'Accumulate n'utilise pas l'interpolation pour rééchantillonner la série temporelle par rapport à l'incrément temporel minimal.

In[7]:=

ts2 = Accumulate[TimeSeries[ts1, TemporalRegularity -> True]]

Out[7]=

In[8]:=

DateListStepPlot[ts2, Joined -> False, PlotTheme -> "Detailed"]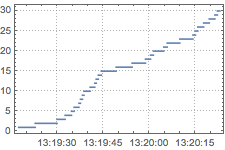

Out[8]=

Calculez le paramètre de PoissonProcess à partir du signal et comparez le paramètre d'ExponentialDistribution utilisée pour simuler l'horodatage.

In[9]:=

{FindProcessParameters[ts2, PoissonProcess[\[Mu]]], \[Lambda]}

Out[9]=