Уравнение времени

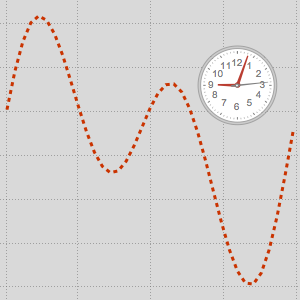
Благодаря нецентральности земной орбиты и отклонению оси по отношению к орбитальной плоскости, видимое движение Солнца меняется в течение года. Это приводит к отклонениям во временных значениях, полученных солнечными часами (истинное солнечное время) по сравнению с более точными часами, например, теми, которые выдают время, определённое видимым вращением неподвижных звёзд (звёздное время). Данная разность известна как уравнение времени.

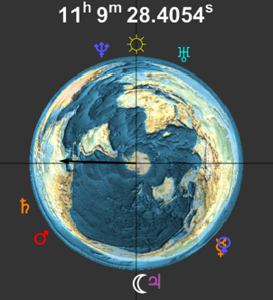
SiderealTime выдаёт значения звёзного времени в смешанных величинах, используя MixedUnit.

In[1]:=

SiderealTime[]

Out[1]=

In[2]:=

SiderealTime[]; QuantityUnit[%]

Out[2]=

Звёздное время по сути является углом и, таким образом, может быть переведено в единицы измерения углов.

In[3]:=

UnitConvert[SiderealTime[], "AngularDegrees"]

Out[3]=

Уравнение времени определено движением Солнца, заданным SunPosition. Рассчитайте недельные значения в полдень по горному времени.

In[4]:=

dates = DateRange[ DateObject[{2015, 1, 1}, TimeObject[{12, 0}, TimeZone -> 0], TimeZone -> 0.`], DateObject[{2015, 12, 31}, TimeObject[{12, 0}, TimeZone -> 0], TimeZone -> 0.`], 7];

In[5]:=

sunpos = SunPosition[GeoPosition[{0, 0}], dates, CelestialSystem -> "Equatorial"]

Out[5]=

Используйте SiderealTime для расчёта прямого восхождения по меридиану Гринвича для этих же дат.

In[6]:=

stime = SiderealTime[GeoPosition[{0, 0}], dates]

Out[6]=

И, наконец, найдите соответствующие значения уравнения времени как разницу между прямым восхождением Солнца и звёздным временем в полдень в течение года. Выразите результат в минутах.

In[7]:=

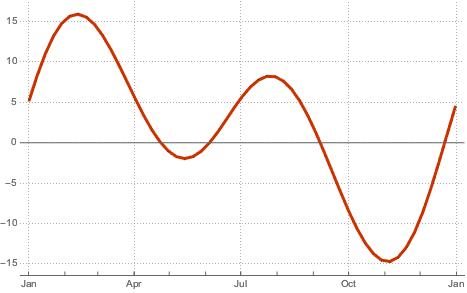
equationoftime = UnitConvert[(TimeSeriesMap[First, sunpos] - stime), "MinutesOfRightAscension"]

Out[7]=

Абсолютные значения уравнения времени могут быть больше 15 минут.

In[8]:=

MinMax[equationoftime]

Out[8]=

In[9]:=

DateListPlot[equationoftime, GridLines -> Automatic, Axes -> True, PlotTheme -> "Web"]

Out[9]=