La ecuación del tiempo
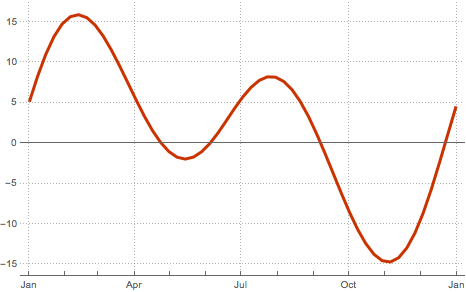
Debido a la excentricidad de la órbita de la Tierra y la inclinación del eje de la Tierra con respecto al plano de la órbita, el aparente movimiento del Sol varía a lo largo del año. Esto induce una variación en el tiempo medido por un reloj solar (tiempo solar aparente) en relación con un reloj más preciso, por ejemplo, uno determinado por la aparente rotación de las estrellas fijas (tiempo sideral). Esta diferencia es conocida como la Ecuación del Tiempo.
SiderealTime regresa valores de tiempo sideral como cantidades de unidades mixtas, usando MixedUnit.
SiderealTime[]SiderealTime[];
QuantityUnit[%]Un tiempo sideral es realmente un ángulo y, por lo tanto, puede ser convertido en otras unidades angulares.
UnitConvert[SiderealTime[], "AngularDegrees"]La Ecuación del Tiempo es determinada por el movimiento del Sol, dada por SunPosition. Calcule valores semanales al mediodía GMT.

dates = DateRange[
DateObject[{2015, 1, 1}, TimeObject[{12, 0}, TimeZone -> 0],
TimeZone -> 0.`],
DateObject[{2015, 12, 31}, TimeObject[{12, 0}, TimeZone -> 0],
TimeZone -> 0.`], 7];sunpos = SunPosition[GeoPosition[{0, 0}], dates,
CelestialSystem -> "Equatorial"]Utilice SiderealTime para calcular la ascensión recta en el meridiano de Greenwich para las mismas fechas semanales.
stime = SiderealTime[GeoPosition[{0, 0}], dates]Finalmente, encuentre los valores correspondientes de la Ecuación del Tiempo como la diferencia entre la ascensión recta del Sol y el tiempo sideral a mediodía durante el año. Exprese el resultado en minutos.
equationoftime =
UnitConvert[(TimeSeriesMap[First, sunpos] - stime),
"MinutesOfRightAscension"]Los valores absolutos de la Ecuación del Tiempo pueden ser mayores que 15 minutos.
MinMax[equationoftime]