Accelerate Mandelbrot Set Computation
The Wolfram Compiler supports a broad set of Wolfram Language functions for numerical computation such as Plus, Power, Sin, etc., as well as many programming constructs. Strong type inference rules allow the output type of variables to be deduced automatically.
The following function computes the number of iterations required to escape beyond the critical value 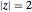 that defines the Mandelbrot set. Note that Function declares the input to be a complex variable using the new annotation Typed.
that defines the Mandelbrot set. Note that Function declares the input to be a complex variable using the new annotation Typed.
FunctionCompile determines that the input is a complex number from the Typed annotation but automatically deduces that the output is an integer.
Measure how long it takes to apply each function to a grid in the complex plane.
The two results are identical.
However, the compiled function provides a greater than factor of forty speedup.
Visualize the grid of results using ArrayPlot and a five-times finer grid.