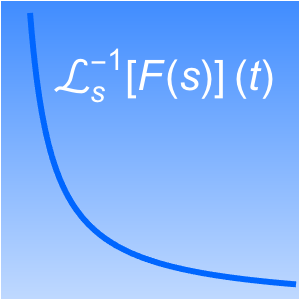
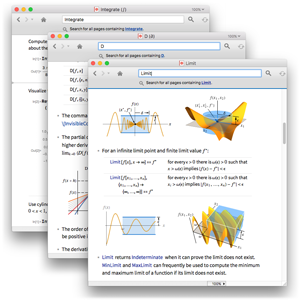
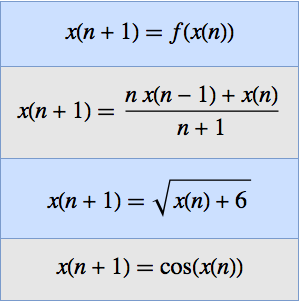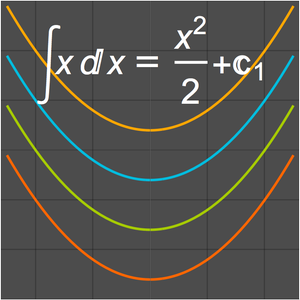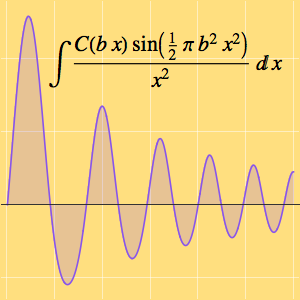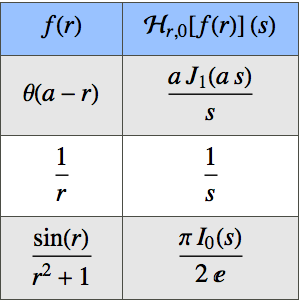Find Lower and Upper Limits of Multivariate Functions
Version 12 of the Wolfram Language introduces completely new functionality for computing lower and upper limits of multivariate functions, based on newly developed algorithms. Lower and upper limits of real-valued functions always exist, even when the limit does not exist, hence the new functionality allows for more detailed analysis of local behavior of functions.
Investigate the limit behavior of a bivariate function 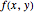 near zero.
near zero.
Show that the limit of 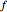 at zero does not exist.
at zero does not exist.
Compute the lower limit and the upper limit of 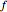 at zero.
at zero.
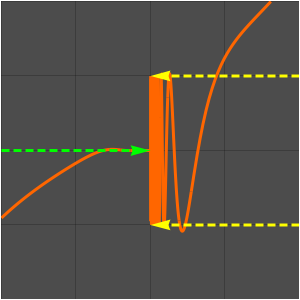
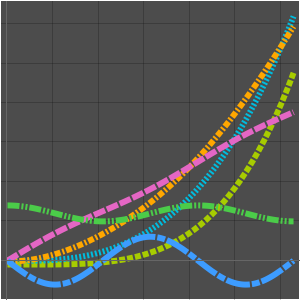
Visualize the result.
show complete Wolfram Language input