Most Efficient Containers of Given Shape
The "Solid" entity domain contains closed regions in space that are of mathematical interest.
Many properties are available for each solid.
Naturally, two of these properties are surface area and volume.
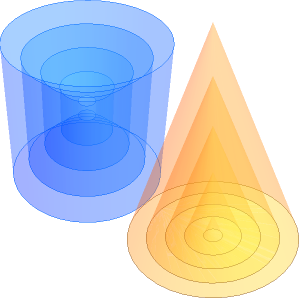
As is well known, the ratio of surface area to volume is minimized over all possible shapes by the filled sphere (ball). However, it is also interesting to consider the parameters that minimize the surface area needed to enclose a fixed volume for other families of solids. For example, it is straightforward to show that the solid cylinder that most efficiently encloses its volume has a height-to-base radius ratio of  (or equivalently, a base diameter equal to its height).
(or equivalently, a base diameter equal to its height).
You can also consider other solids, where for simplicity the volume is fixed to unity.
Of all cuboids, the cube (i.e. equilateral cuboid) gives the greatest volume contained per surface area.
A trirectangular tetrahedron also has the smallest surface area for a given volume enclosed when its edge lengths along the Cartesian axes are equal.
For a solid cone, the surface area–minimizing dimensions can also be calculated in closed form.
You can now visualize the most efficient solids for these shapes as the overall dimensions are varied.