Investigate the Riemann Hypothesis

First published in a groundbreaking 1859 paper by Bernhard Riemann, the Riemann hypothesis is a deep mathematical conjecture that states that the nontrivial Riemann zeta function zeros, i.e. the values of the Riemann zeta function

other than 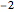, , 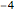, 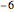… such that 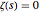all lie on the "critical line" 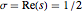, where 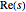denotes the real part of of a complex variable .

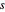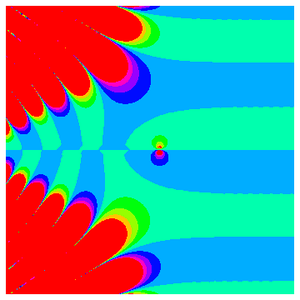
While the Riemann zeta function oscillates infinitely along the negative real axis, it asymptotically approaches 1 along the positive real axis.

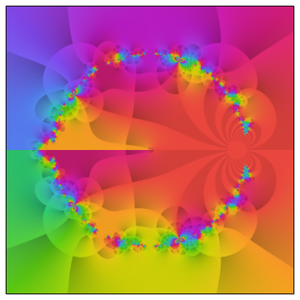
The behavior gets even more complicated along the critical line.

In fact, the preceding plot gives a more representative idea of the true complexity that arises in the complex plane.

The first 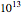nontrivial zeros of the Riemann zeta function have been tested and found to satisfy the Riemann hypothesis. It is therefore rather surprising that despite such abundant numerical evidence and despite considerable effort, no one has been able to prove the hypothesis over the last 250 years.

Many results in mathematics are known "assuming the Riemann hypothesis holds". This means a proof of the Riemann hypothesis would immediately establish a multitude of other results in mathematics. There are also many alternate formulations of the Riemann hypothesis, a collection that the RiemannHypothesisFormulation entity domain attempts to collect.

The collection currently contains a total of roughly 70 formulations.

These formulations can in turn be grouped into about half that many families.

The original form of the Riemann hypothesis can be stated using quantifier arithmetic in the following concise form.

While in principle this is a computable expression, since no one knows how to establish the Riemann hypothesis, applying quantifier elimination to it turns unevaluated (after all, if Mathematica could resolve the quantifiers in this case, it would be capable of establishing the validity of the Riemann hypothesis).

Now examine the types of alternate formulations present in the RiemannHypothesisFormulation domain.

Perhaps the most famous alternate statement of the Riemann hypothesis concerns the positivity of expressions given by derivatives of the 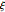-function—a function closely related to 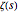—is Li's inequality. This formulation, known as Li's inequality, can be formally stated as follows.

The Wolfram Language can directly compute closed forms for the expression inside the inequality (though doing so for large indices requires use of known recurrence relations satisfied by the derivatives of 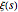). To begin, first extract the inequality from the formulation.

Now define Li's constants whose positivity for all positive is equivalent to the Riemann hypothesis.

Computing exactly and numericizing the constants up to order five verifies they are indeed positive.

Of course, Li's inequality is just one alternate formulation. A number of mathematicians have derived multiple formulations for the Riemann hypothesis. Here is a list of formulators ordered by the number of distinct formulations represented in the collection.

You can now construct a timeline of investigators that illustrates to some degree the high level of activity that has been devoted to Riemann's beautiful yet stubborn hypothesis.