Contenedores más eficientes de forma predeterminada
El dominio de la entidad "Solid"contiene regiones cerradas en el espacio que son de interés matemático.
Muchas propiedades están disponibles para cada sólido.
Naturalmente, dos de estas propiedades son el área de la superficie y el volumen.
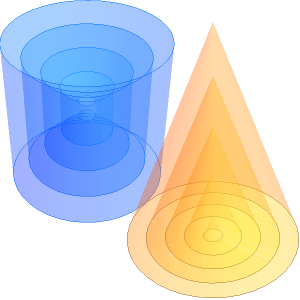
Como es bien sabido, la relación del área de la superficie a volumen se minimiza sobre todas las formas posibles por una esfera llena (bola). Sin embargo, también es interesante considerar los parámetros que minimizan el área de la superficie necesaria para encerrar un volumen fijo para otras familias de sólidos. Por ejemplo, es sencillo demostrar que un cilindro sólido que encierra más eficientemente su volumen tiene una relación de radio de altura a base de 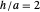 (o equivalente, el diámetro de la base es igual a su altura).
(o equivalente, el diámetro de la base es igual a su altura).
También puede considerar otros sólidos, donde por simplicidad el volumen está fijado a la unidad.
De todos los cuboides, el cubo (es decir, cuboide equilátero) da el mayor volumen contenido por área de superficie.
Un tetraedro trirectangular también tiene el área de la superficie más pequeña para un volumen dado encerrado cuando sus longitudes de borde a lo largo de los ejes cartesianos son iguales.
Para un cono sólido, las dimensiones de minimización del área de la superficie también se pueden calcular en forma cerrada.
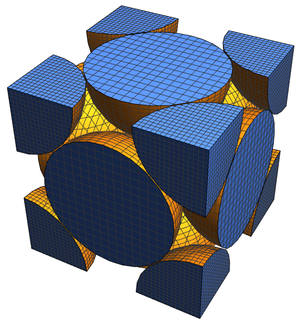
Ahora puede visualizar los sólidos más eficientes para estas formas a medida que varían las dimensiones generales.