Explore Group Relations and Generators

The "FiniteGroup" entity domain catalogs detailed data on notable groups of finite order.

The list of groups includes the 23 sporadic groups, the largest of which is the Monster group and the first several of which are tabulated here together with their group orders.

A number of interesting visualizations can be made of finite groups. A simple one plots the multiplication table using ArrayPlot, revealing band and block structure in the underlying representations.

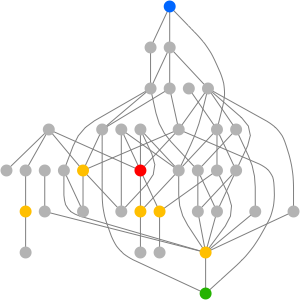
The Cayley graph is another way to visualize groups. The Cayley graph associated with a given graph and generating set is defined as the directed graph having one vertex associated with each group element and directed edges 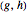whenever is a member of a generating set. (The Cayley graph may depend on the choice of a generating set.)

For example, the Cayley graph of the Abelian group 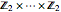is given by the bidirected hypercube graph .

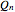The correspondence with the hypercube graph can be verified using ToEntity, which returns the corresponding hypercube "Graph" entities.

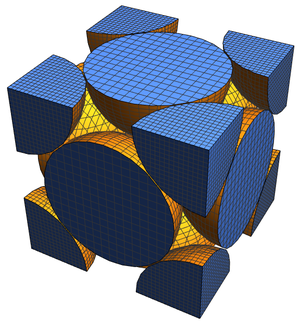
Cayley graphs of the tetrahedral crystallographic point groups correspond to named graphs derived from the skeletons of semiregular (Archimedean) polyhedra.

Again, the associated graphs can be programmatically obtained.

These in turn can be converted to entities in the "Polyhedron" entity domain that have skeletons corresponding to these graphs.