模拟带电三角板的场线
Wolfram 语言既是一种强大的计算语言,也是人们进行科学交流的有效语言。一个很好的例子是在物理系统的实体领域。要了解 "PhysicalSystem" 涵盖的范围,请查看以下可用实体样本:
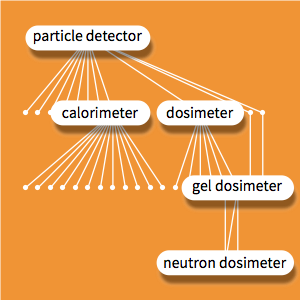
通过将它们分类为实体类别来简化查找给定的感兴趣的物理系统。目前有 27 个非不相交的实体类,下面显示其中一个样本。
物理系统主要包含能在教科书中找到的公式,而不是如 "Country" 类数据那样主要包含数字或文本数据。要了解如何使用这些数据,我们来看一个带电的三角板。
通过调用 "NonMissingProperties" 来查看该实体可用的内容。
通常,"PhysicalSystem" 中的实体与一组描述系统的整体物理参数的 "system variables" 相关联。对于空间中的带电三角板,这些变量为板子的电荷 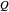 、顶点的坐标
、顶点的坐标 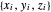 ,
,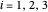 。
。
任何给定的属性可能取决于这些系统变量,也可能取决于系统的广义坐标。例如,下面来查看电荷密度。
注意,对于 "PhysicalSystem" 返回的公式,表达式的标头通常为 Inactive[ReplaceRepeated]。因而允许使用中间变量,可以使这些表达式更简短,更容易理解。例如,在前面提到的公式中,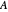 是三角形的面积,
是三角形的面积,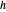 表示从三角形到测量点的垂直距离。DiracDelta 和 Piecewise 表示电荷密度仅在(无限薄)三角板上非零。替换后,表达式将简化为仅涉及系统变量和广义坐标的表达式。
表示从三角形到测量点的垂直距离。DiracDelta 和 Piecewise 表示电荷密度仅在(无限薄)三角板上非零。替换后,表达式将简化为仅涉及系统变量和广义坐标的表达式。
一个更有趣的属性可能是带电薄板的电场。为简化起见,请考虑二维薄板(假定 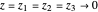 )。 可使用以下 EntityValue 调用求出电场(结果在此处被抑制,因为比较大)。
)。 可使用以下 EntityValue 调用求出电场(结果在此处被抑制,因为比较大)。
选择一个感兴趣的三角板,将其顶点坐标代入 fieldForm 并激活,即可产生一个电场向量的解析解,它是 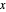 -
-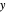 平面上坐标的函数。
平面上坐标的函数。
上面的表达式相当复杂,因此为了便于显示,可以通过 TraditionalForm Pane 呈现。
最后一步,尝试可视化根据这些公式得出的场线。幸运的是,Wolfram 语言中有内置函数 StreamDensityPlot,可以完成这项工作。在绘制之前,要仔细地删除前面表达式中的 QuantityVariable 项,下面将演示如何执行此替换。此外,为了使图形更有趣,叠加两个带电三角板,并构建一个 Manipulate,显示电场如何随它们的相互位置、角度和电荷的变化而相互作用。查看代码和生成的动画,享受使用 Wolfram 语言模拟物理系统的乐趣!