Elementos de Euclides
Uno de los tratados matemáticos más antiguos e influyentes de todos los tiempos son los Elementos, una serie de trece libros del antiguo matemático griego Euclides de Alejandría. Las construcciones descritas en los Elementos se pueden representar en Wolfram Language utilizando GeometricScene y pueden ser visualizados con RandomInstance.
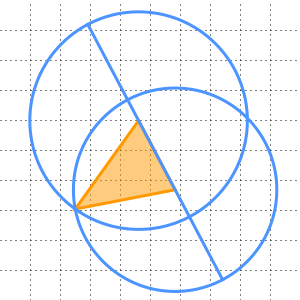
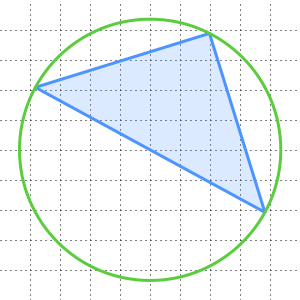
La Proposición 1 del Libro I establece que, dados dos puntos 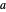 y
y 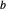 cualesquiera, se puede construir un triángulo equilátero con
cualesquiera, se puede construir un triángulo equilátero con 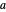 y
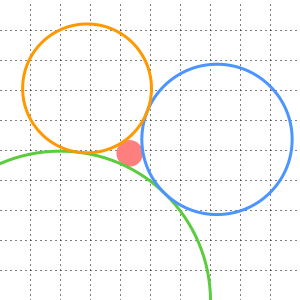
y 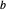 como dos de sus vértices. En particular, se pueden dibujar dos círculos centrados en
como dos de sus vértices. En particular, se pueden dibujar dos círculos centrados en 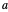 y
y 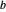 respectivamente, cuyos radios sean iguales a la distancia entre ellos. Su punto de intersección
respectivamente, cuyos radios sean iguales a la distancia entre ellos. Su punto de intersección 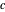 forma el tercer vértice de dicho triángulo equilátero.
forma el tercer vértice de dicho triángulo equilátero.
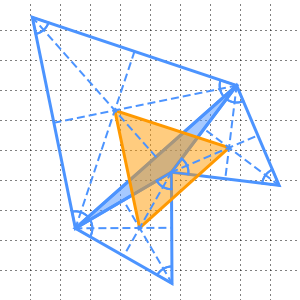
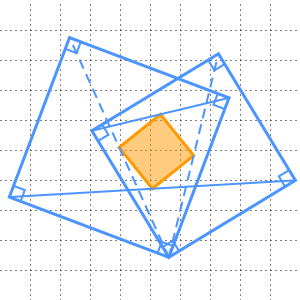
La Proposición 22 del Libro I generaliza la Proposición 1 al afirmar que para cualquier cantidad positiva 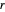 ,
, 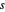 y
y 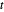 , en las que
, en las que 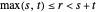 , hay un triángulo con longitudes laterales
, hay un triángulo con longitudes laterales 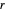 ,
, 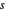 y
y 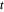 .
.
Elija al azar cantidades positivas 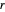 ,
, 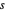 y
y 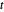 , en las que
, en las que 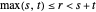 .
.
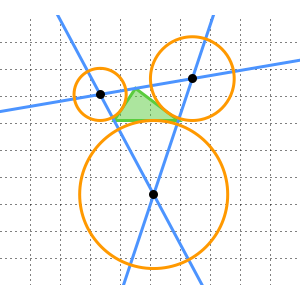
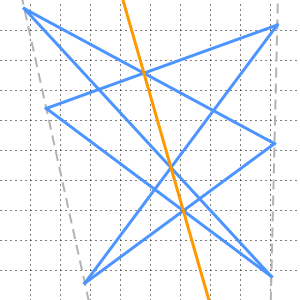
La construcción procede de la siguiente manera: construya una línea recta a través de los puntos 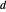 ,
, 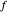 ,
, 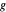 y
y 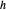 en orden, con las distancias
en orden, con las distancias 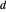 y
y 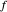 separadas por
separadas por 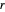 , la distancias
, la distancias 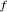 y
y 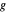 separadas por
separadas por 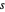 y las distancias
y las distancias 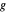 y
y 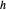 separadas por
separadas por 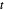 . Dibuje el circulo centrado en
. Dibuje el circulo centrado en 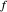 atravesando
atravesando 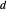 , así como el círculo centrado en
, así como el círculo centrado en 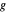 atravesando
atravesando 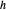 . Si
. Si 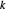 es uno de los puntos donde se cruzan estos círculos, entonces
es uno de los puntos donde se cruzan estos círculos, entonces 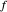 es la distancia
es la distancia 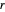 de
de 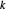 ,
, 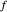 es la distancia
es la distancia 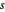 de
de 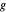 y
y 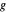 es la distancia
es la distancia 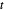 de
de 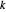 . Por tanto, los puntos
. Por tanto, los puntos 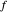 ,
, 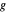 y
y 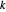 formar dicho triángulo.
formar dicho triángulo.