Spatial Statistics on the Surface of the Earth
The spatial median of a dataset gives a point with minimum total distance to every point in the data: 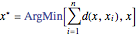 , which may not belong to the original dataset. The central feature, on the other hand, selects a point from a dataset that minimizes the total distance to all other points in the data.
, which may not belong to the original dataset. The central feature, on the other hand, selects a point from a dataset that minimizes the total distance to all other points in the data.
Compute the spatial median and central feature of several cities on the surface of the Earth.
Find the coordinates of the cities.
Compute the spatial median.
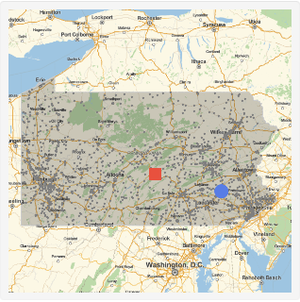
Use a centered geo projection to visualize the result.
Identify the country where the spatial median is located.
Compute the central feature.
The central feature can also be computed directly from the list of cities.
Find the distance between the spatial median and the central feature.
The total distance between the spatial median and the data points is not greater then the total distance between the central feature and the data points.
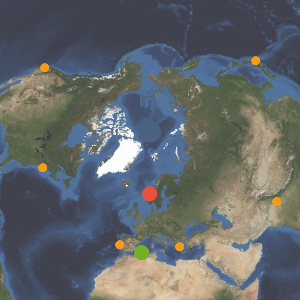
When working with GeoPosition or equivalent input, the spatial median and central feature use GeoDistance as a distance function, which takes into account that the Earth is a curved closed surface. Working in the latitude-longitude space gives the wrong result.
Compute the spatial median in the latitude-longitude space.
Find which country is the closest.
Visualize how far apart both medians are.