When Mean Is Useless—Robust Location Measures

Heavy-tail distributions, like Cauchy or Pareto distributions, carry significant probability measure (weight) in their tails, which means that rarely occurring events have non-negligible probability. Such distributions often have some undefined moments, for example, mean. You can use robust measures like the trimmed or winsorized mean to estimate the central location of the distribution.

Robust location and dispersion measures in Version 12.

Have a look at an example of a heavy-tailed distribution.

The mean is not defined.

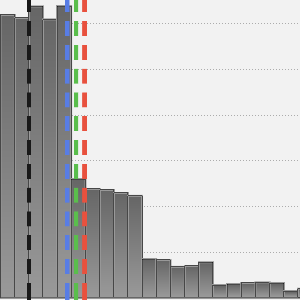
This is a heavy-tailed distribution and most of the weight is in the tail. Compute the quartiles.

Compute the mean after removing 10% of the long tail.

This corresponds to truncating the distribution.

Compute the mean after clipping 10% of the long tail.

This corresponds to censoring.

The difference between discarding 10% of the largest values and clipping them is significant, which accounts for the "heavy tail" of this distribution.