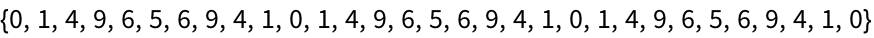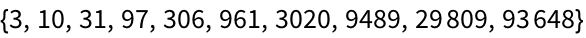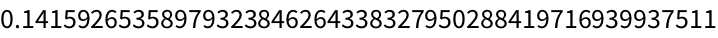When you do a computation with whole numbers, the Wolfram Language gives you an exact answer. It does the same with exact fractions.
Adding 1/2+1/3 gives an exact answer as a fraction:
Often you
’ll just want a numerical or decimal approximation. You can get that using the function
N (for
“numerical
”).
Get an approximate numerical answer:
If there’s any decimal number in your input, the Wolfram Language will automatically give you an approximate answer.
The presence of a decimal number makes the result be approximate:
It
’s enough just to have a decimal point at the end of a number:
The Wolfram Language can handle numbers of any size, at least so long as they fit in your computer
’s memory.
Here’s 2 raised to the power 1000:
Get a numerical approximation:
This approximate form is given in
scientific notation. If you need to enter scientific notation, you can do it with *^.
Enter a number in scientific notation:
Commonly used numbers like
π (pi) are built into the Wolfram Language.
Get a numerical approximation to π:
The Wolfram Language can compute to
arbitrary precision, so for example it can find millions of digits of
π if you want them.
Compute 250 digits of π:
There are many functions in the Wolfram Language that handle
integers (whole numbers). There are also many functions that handle
real numbers—approximate numbers with decimals. An example is
RandomReal, which gives random real numbers.
Generate a random real number in the range 0 to 10:
Generate 5 random real numbers:
An alternative way to ask for 5 random real numbers:
Random real numbers in the range 20 to 30:
The Wolfram Language has a huge range of mathematical functions built in, from basic to very sophisticated.
Find the 100th prime number:
Find the millionth prime number:
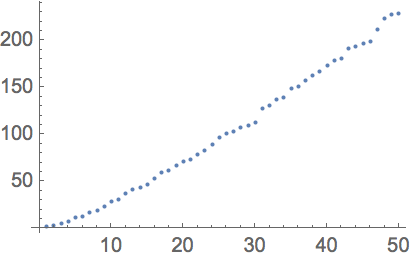
Plot the first 50 primes:
Three functions common in many practical situations are
Sqrt (square root),
Log10 (logarithm to base 10) and
Log (natural logarithm).
The square root of 16 is 4:
If you don’t ask for a numerical approximation, you’ll get an exact formula:
N gives a numerical approximation:
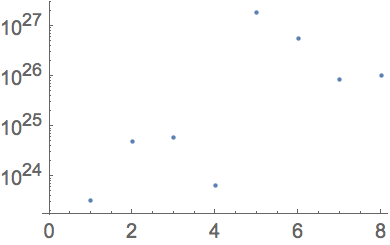
Logarithms are often useful when you
’re dealing with numbers that have a wide range of sizes. Let
’s plot the masses of the planets. With
ListPlot one can
’t tell anything about the planets before Jupiter. But
ListLogPlot shows the relative sizes much more clearly.
Make an ordinary
ListPlot of the masses of the planets:
There are a few more functions that show up frequently in general programming. First, there
’s the almost trivial function
Abs, that finds the absolute value, or positive part, of a number.
Abs effectively just drops minus signs:
Next there
’s
Round, which rounds to the nearest whole number.
Round rounds to the nearest whole number:
Another function that
’s very useful is
Mod. Let
’s say you
’re counting up minutes in an hour. When you reach 60, you
’ll want to start again from 0. That
’s what
Mod lets you do.
Compute a sequence of numbers mod 60:
| N[expr] | | numerical approximation |
| Pi | | the number π (pi)≃3.14 |
| Sqrt[x] | | square root |
| Log10[x] | | logarithm to base 10 |
| Log[x] | | natural logarithm (ln) |
| Abs[x] | | absolute value (drop minus signs) |
| Round[x] | | round to nearest integer |
| Prime[n] | | nth prime number |
| Mod[x,n] | | modulo (“clock arithmetic”) |
| RandomReal[max] | | random real number between 0 and max |
| RandomReal[max,n] | | list of n random real numbers |
| ListLogPlot[data] | | plot on a logarithmic scale |
23.1Find
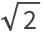
to 500-digit precision.
»
23.2Generate 10 random real numbers between 0 and 1.
»
23.3Make a plot of 200 points with random real
x and
y coordinates between 0 and 1.
»
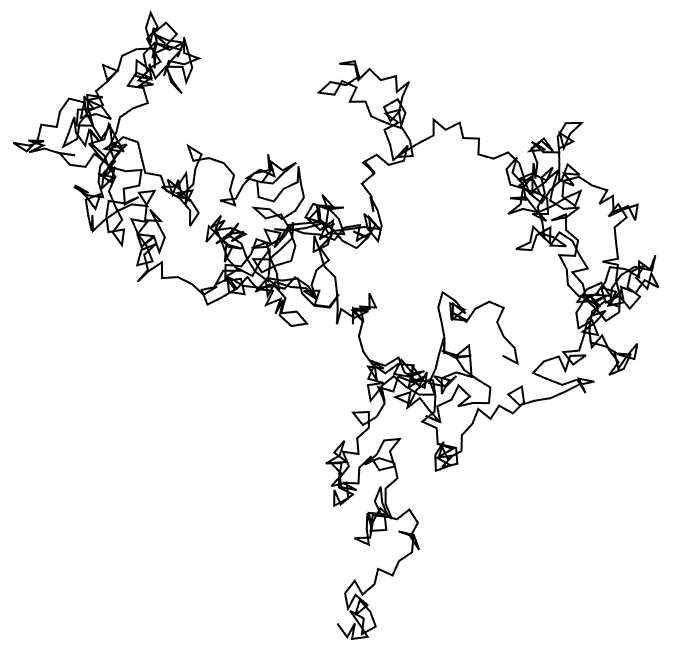
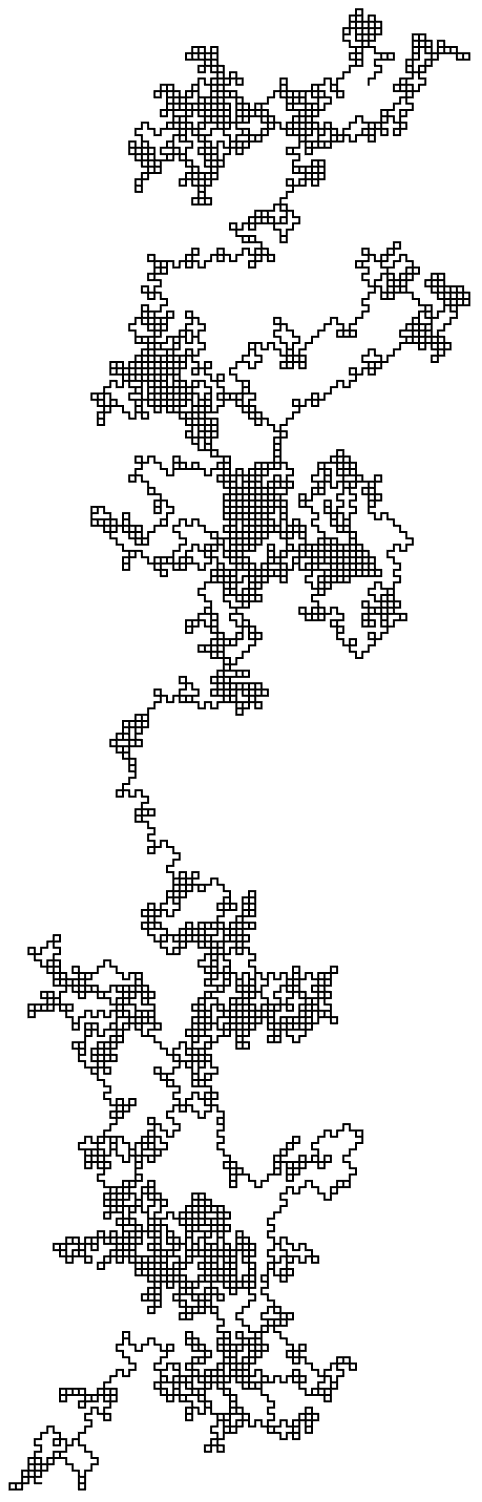
23.4Create a random walk using
AnglePath and 1000 random real numbers between 0 and 2
π.
»
23.5Make a table of
Mod[n^2, 10] for
n from 0 to 30.
»
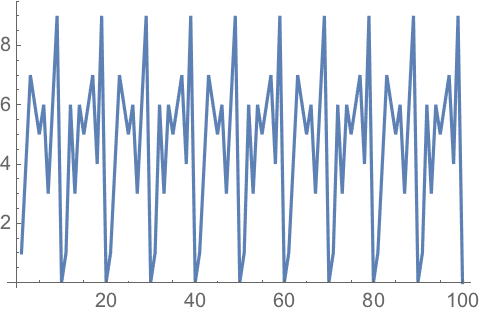
23.6Make a line plot of
Mod[n^n, 10] for
n from 1 to 100.
»
23.7Make a table of the first 10 powers of
π, rounded to integers.
»
23.8Make a graph by connecting
n with
Mod[n^2, 100] for
n from 0 to 99.
»
23.9Generate graphics of 50 circles with random real coordinates 0 to 10, random real radii from 0 to 2, and random colors.
»
23.10 Make a plot of the
nth prime divided by
n*log(n), for
n from 2 to 1000.
»
23.11Make a line plot of the differences between successive primes up to 100.
»
23.12Generate a sequence of 20 middle C notes with random durations between 0 and 0.5 seconds.
»
23.13Make an array plot of
Mod[i, j] for
i and
j up to 50.
»
23.14Make a list for
n from 2 to 10 of array plots for
x and
y up to 50 of
x^y mod n.
»
+23.1Use
Round to compute the fractional part of
π to 50 digits.
»
+23.2Find the sum of the first 1000 prime numbers.
»
+23.3Make a list of the first 100 primes modulo 4.
»
+23.4Make a list of the first 10000 primes modulo 4, multiply them by 90
° and create an angle path from them.
»
What are examples of mathematical functions in the Wolfram Language?
From standard school math, ones like
Sin,
Cos,
ArcTan,
Exp, as well as
GCD,
Factorial,
Fibonacci. From physics and engineering and higher math, ones like
Gamma (
“gamma function
”),
BesselJ (
“Bessel function
”),
EllipticK (
“elliptic integral
”),
Zeta (
“Riemann zeta function
”),
PrimePi,
EulerPhi. From statistics, ones like
Erf,
NormalDistribution,
ChiSquareDistribution. Hundreds of functions altogether.
What is the precision of a number?
It
’s the total number of decimal digits quoted in the number.
N[100/3, 5] gives
33.333, which has 5 digits of precision. The number
100/3 is exact;
N[100/3, 5] approximates it to 5-digit precision.
What does the
at the end of each line in a long number mean?
It’s there to show that the number continues onto the next line—like a hyphen in text.
Can I work with numbers in bases other than 10?
Yes. Enter a number in base 16 as
16^^ffa5. Find digits using
IntegerDigits[655, 16].
Can the Wolfram Language handle complex numbers?
Of course. The symbol
I (capital
“i
”) represents the square root of
−1.
Why does
N[1.5/7, 100] not give me a 100-digit result?
Because
1.5 is an approximate number with much less than 100-digit precision.
N[15/70, 100] will for example give a 100-digit-precision number.
- The Wolfram Language does “arbitrary-precision computation”, meaning that it can keep as many digits in a number as you want.
- When you generate a number with a certain precision using N, the Wolfram Language will automatically keep track of how that precision is affected by computations—so you don’t have to do your own numerical analysis of roundoff errors.
- If you type a number like 1.5, it’s assumed to be at the native “machine precision” of numbers on your computer (usually about 16 digits, though only 6 are usually displayed). Use 1.5 `100 to specify 100-digit precision.
- With exact input (like 4 or 2/3 or Pi), the Wolfram Language always tries to give exact output. But if the input contains an approximate number (like 2.3), or if you use N, it’ll use numerical approximation.
- Numerical approximation is often crucial in making large-scale computations feasible.
- PrimeQ tests if a number is prime (see Section 28). FactorInteger finds the factors of an integer.
- RandomReal can give numbers that aren’t just uniformly distributed. For example, RandomReal[NormalDistribution[ ]] gives normally distributed numbers.
- Round rounds to the nearest integer (up or down); Floor always rounds down; Ceiling always rounds up.
- RealDigits is the analog of IntegerDigits for real numbers.