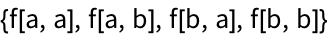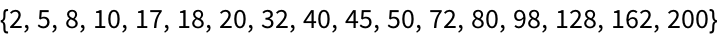WOLFRAM

Explore the latest version of An Elementary Introduction to the Wolfram Language »
Stephen Wolfram
An Elementary Introduction to the Wolfram Language
Second Edition (2017)
33Expressions and Their Structure
We’ve now seen all sorts of things that exist in the Wolfram Language: lists, graphics, pure functions and much more. And now we’re ready to discuss a very fundamental fact about the Wolfram Language: that each of these things—and in fact everything the language deals with—is ultimately constructed in the same basic kind of way. Everything is what’s called a symbolic expression.
Symbolic expressions are a very general way to represent structure, potentially with meaning associated with that structure. f[x,y] is a simple example of a symbolic expression. On its own, this symbolic expression doesn’t have any particular meaning attached, and if you type it into the Wolfram Language, it’ll just come back unchanged.
f[x, y] is a symbolic expression with no particular meaning attached:
In[1]:=
Click for copyable input
Out[1]=
{x,y,z} is another symbolic expression. Internally, it’s List[x,y,z], but it’s displayed as {x,y,z}.
The symbolic expression List[x, y, z] displays as {x, y, z}:
In[2]:=
Click for copyable input
Out[2]=
Symbolic expressions are often nested:
In[3]:=
Click for copyable input
Out[3]=
FullForm shows you the internal form of any symbolic expression.
In[4]:=
Click for copyable input
Out[4]//FullForm=
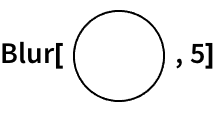
Graphics[Circle[{0,0}]] is another symbolic expression, that just happens to display as a picture of a circle. FullForm shows its internal structure.
This symbolic expression displays as a circle:
In[5]:=
Click for copyable input
Out[5]=
FullForm shows its underlying symbolic expression structure:
In[6]:=
Click for copyable input
Out[6]//FullForm=
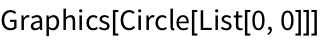Symbolic expressions often don’t just display in special ways, they actually evaluate to give results.
A symbolic expression that evaluates to give a result:
In[7]:=
Click for copyable input
Out[7]=
The elements of the list evaluate, but the list itself stays symbolic:
In[8]:=
Click for copyable input
Out[8]=
Here’s the symbolic expression structure of the list:
In[9]:=
Click for copyable input
Out[9]//FullForm=
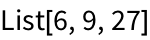This is just a symbolic expression that happens to evaluate:
In[10]:=
Click for copyable input
Out[10]=
You could write it like this:
In[11]:=
Click for copyable input
Out[11]=
What are the ultimate building blocks of symbolic expressions? They’re called atoms (after the building blocks of physical materials). The main kinds of atoms are numbers, strings and symbols.
Things like x, y, f, Plus, Graphics and Table are all symbols. Every symbol has a unique name. Sometimes it’ll also have a meaning attached. Sometimes it’ll be associated with evaluation. Sometimes it’ll just be part of defining a structure that other functions can use. But it doesn’t have to have any of those things; it just has to have a name.
A crucial defining feature of the Wolfram Language is that it can handle symbols purely as symbols—“symbolically”—without them having to evaluate, say to numbers.
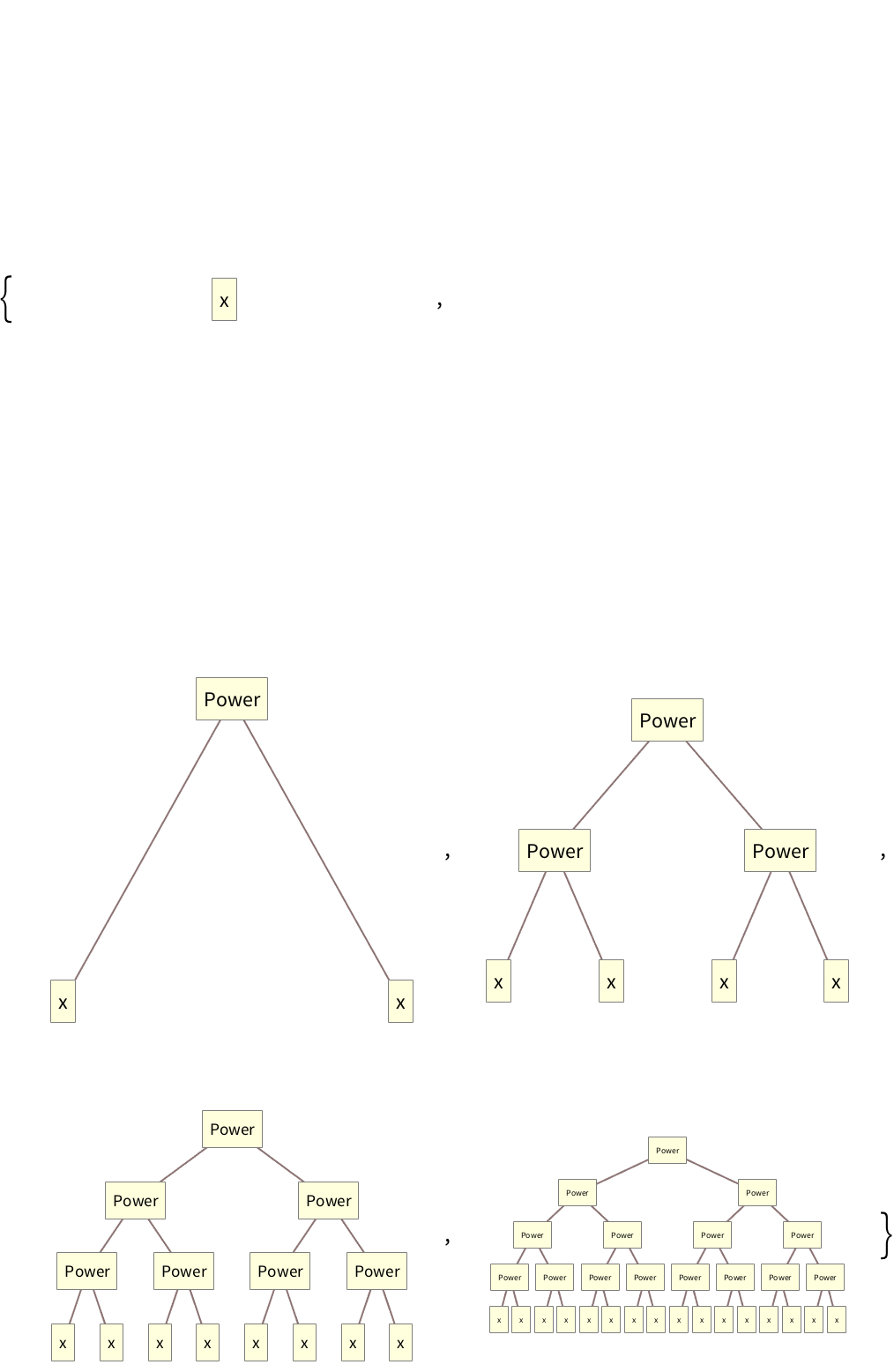
In the Wolfram Language, x can just be x, without having to evaluate to anything:
In[12]:=
Click for copyable input
Out[12]=
x does not evaluate, but the addition is still done, here according to the laws of algebra:
In[13]:=
Click for copyable input
Out[13]=
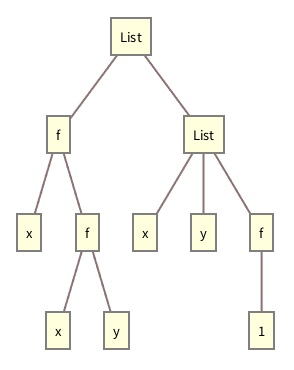
Given symbols like x, y and f, one can build up an infinite number of expressions from them. There’s f[x], and f[y], and f[x,y]. Then there’s f[f[x]] or f[x,f[x,y]], or, for that matter, x[x][y,f[x]] or whatever.
In general, each expression corresponds to a tree, whose ultimate “leaves” are atoms. You can display an expression as a tree using TreeForm.
An expression shown in tree form:
In[14]:=
Click for copyable input
Out[14]//TreeForm=
Here’s a graphics expression shown in tree form:
In[15]:=
Click for copyable input
Out[15]//TreeForm=
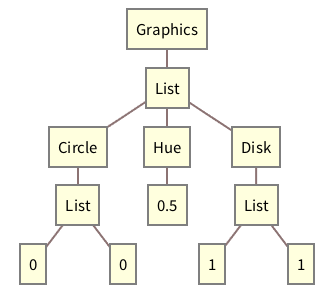Because expressions ultimately have a very uniform structure, operations in the Wolfram Language operate in a very uniform way on them.
For example, any expression has parts, just like a list, and you can extract them using [[...]].
This is equivalent to {x, y, z}[[2]], which extracts the second element in a list:
In[16]:=
Click for copyable input
Out[16]=
Extracting parts works exactly the same way for this expression:
In[17]:=
Click for copyable input
Out[17]=
This extracts the circle from the graphics:
In[18]:=
Click for copyable input
Out[18]=
This goes on and extracts the coordinates of its center:
In[19]:=
Click for copyable input
Out[19]=
This works exactly the same:
In[20]:=
Click for copyable input
Out[20]=
In f[x,y], f is called the head of the expression. x and y are called arguments. The function Head extracts the head of an expression.
The head of a list is List:
In[21]:=
Click for copyable input
Out[21]=
Every part of an expression has a head, even its atoms.
The head of an integer is Integer:
In[22]:=
Click for copyable input
Out[22]=
The head of an approximate real number is Real:
In[23]:=
Click for copyable input
Out[23]=
The head of a string is String:
In[24]:=
Click for copyable input
Out[24]=
Even symbols have a head: Symbol.
In[25]:=
Click for copyable input
Out[25]=
In patterns, you can ask to match expressions with particular heads. _Integer represents any integer, _String any string and so on.
_Integer is a pattern that matches only objects with head Integer:
In[26]:=
Click for copyable input
Out[26]=
Named patterns can have specified heads too:
In[27]:=
Click for copyable input
Out[27]=
In using the Wolfram Language, most of the heads you’ll see are symbols. But there are important cases where there are more complicated heads. One such case is pure functions—where when you apply a pure function, the pure function appears as the head.
Here is the full form of a pure function (# is Slot[1]):
In[28]:=
Click for copyable input
Out[28]//FullForm=
When you apply the pure function, it appears as a head:
In[29]:=
Click for copyable input
Out[29]=
As you become more sophisticated in Wolfram Language programming, you’ll encounter more and more examples of complicated heads. In fact, many functions that we’ve already discussed have operator forms where they appear as heads—and using them in this way leads to very powerful and elegant styles of programming.
Select appears as a head here:
In[30]:=
Click for copyable input
Out[30]=
Both Cases and Select appear as heads here:
In[31]:=
Click for copyable input
Out[31]=
All the basic structural operations that we have seen for lists work exactly the same for arbitrary expressions.
Length does not care what the head of an expression is; it just counts arguments:
In[32]:=
Click for copyable input
Out[32]=
/@ does not care about the head of an expression either; it just applies a function to the arguments:
In[33]:=
Click for copyable input
Out[33]=
Since there are lots of functions that generate lists, it’s often convenient to build up structures as lists even if eventually one needs to replace the lists with other functions.
@@ effectively replaces the head of the list with f:
In[34]:=
Click for copyable input
Out[34]=
This yields Plus[1, 1, 1, 1], which then evaluates:
In[35]:=
Click for copyable input
Out[35]=
This turns a list into a rule:
In[36]:=
Click for copyable input
Out[36]=
Here’s a simpler alternative, without the explicit pure function:
In[37]:=
Click for copyable input
Out[37]=
A surprisingly common situation is to have a list of lists, and to want to replace the inner lists with some function. It’s possible to do this with @@ and /@. But @@@ provides a convenient direct way to do it.
Replace the inner lists with f:
In[38]:=
Click for copyable input
Out[38]=
Turn the inner lists into rules:
In[39]:=
Click for copyable input
Out[39]=
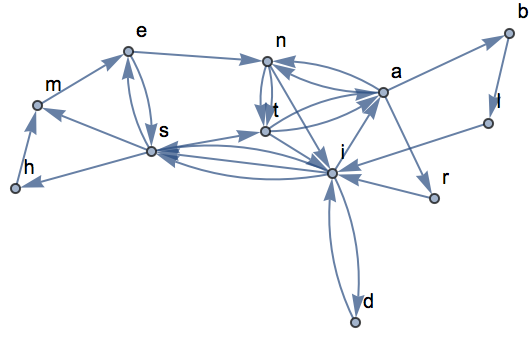
Here’s an example of how @@@ can help construct a graph from a list of pairs.
This generates a list of pairs of characters:
In[40]:=
Click for copyable input
Out[40]=
Turn this into a list of rules:
In[41]:=
Click for copyable input
Out[41]=
Form a transition graph showing how letters follow each other:
In[42]:=
Click for copyable input
Out[42]=
Vocabulary
FullForm[expr] show full internal form
TreeForm[expr] show tree structure
Head[expr] extract the head of an expression
_head match any expression with a particular head
f@@list replace the head of list with f
f@@@{list1,list2, ...} replace heads of list1, list2, ... with f
33.1Find the head of the output from ListPlot. »
Expected output:
Out[]=
33.2Use @@ to compute the result of multiplying together integers up to 100. »
Expected output:
Out[]=
33.3Use @@@ and Tuples to generate {f[a, a], f[a, b], f[b, a], f[b, b]}. »
Expected output:
Out[]=
33.4Make a list of tree forms for the results of 4 successive applications of #^#& starting from x. »
Expected output:
Out[]=
33.5Find the unique cases where i^2/(j^2+1) is an integer, with i and j going up to 20. »
Expected output:
Out[]=
33.6Create a graph that connects successive pairs of numbers in Table[Mod[n^2+n, 100], {n, 100}]. »
Expected output:
Out[]=
33.7Generate a graph showing which word can follow which in the first 200 words of the Wikipedia article on computers. »
Sample expected output:
Out[]=
33.8Find a simpler form for f@@#&/@{{1, 2}, {7, 2}, {5, 4}}. »
Sample expected output:
Out[]=
Q&A
How are @@ and @@@ interpreted?
f@@expr is Apply[f, expr]. f@@@expr is Apply[f, expr, {1}]. They’re usually just read as “double at” and “triple at”.
Are all expressions in the Wolfram Language trees?
At a structural level, yes. When there are variables with values assigned (see Section 38), though, they can behave more like directed graphs. And of course one can use Graph to represent any graph as an expression in the Wolfram Language.
Tech Notes
More to Explore
Guide to Expressions in the Wolfram Language »
 
Download Notebook Version
es