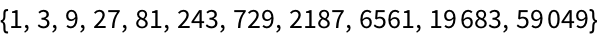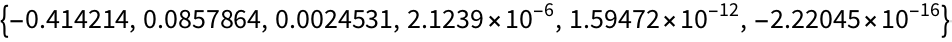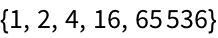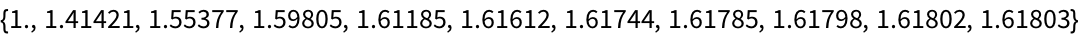| 27 | Applying Functions Repeatedly |
f[x] applies
f to
x.
f[f[x]] applies
f to
f[x], or effectively nests the application of
f. It
’s common to want to repeat or nest a function.
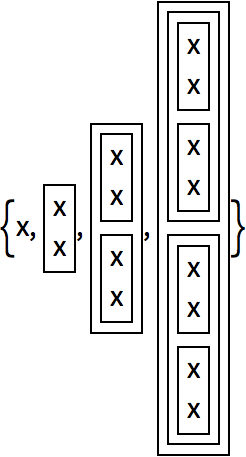
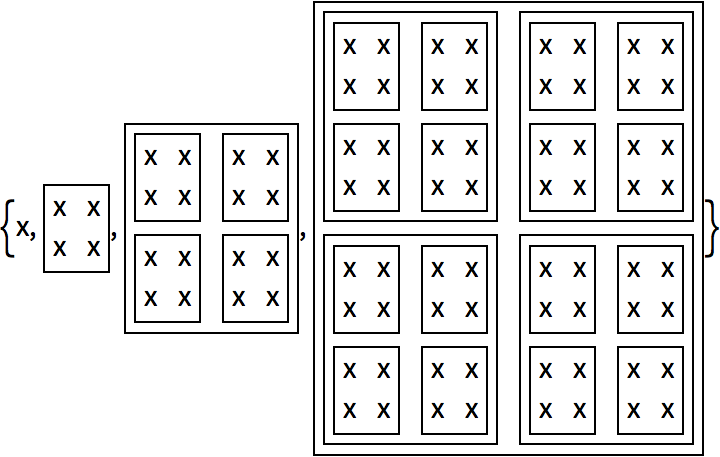
This makes a list of the results of nesting
f up to 4 times:
Using
Framed as the function makes it a little more obvious what
’s going on:
If you want to see a list of the results of successive nestings, use
NestList. If you only want to see the final result, use
Nest.
This gives the final result of 5 levels of nesting:
Nestedly apply
EdgeDetect to an image, first finding edges, then edges of edges and so on.
Nestedly do edge detection on an image:
Use a pure function to both edge-detect and color-negate at each step:
Start with red, and nestedly blend with yellow, getting more and more yellow.
Add another yellow into the blend at each step:
If you successively apply a function that adds 1, you just get successive integers.
Nestedly add 1, getting successive numbers:
Nestedly multiply by 2, getting powers of 2.
The result doubles each time, giving a list of powers of 2:
Nested squaring very soon leads to big numbers:
You can make nested square roots too.
Nestedly apply square root:
The decimal version of the result converges quickly (to the
golden ratio):
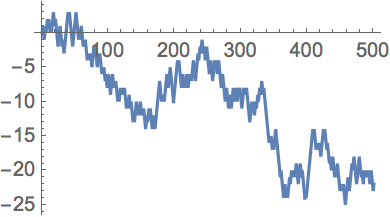
RandomChoice randomly chooses from a list. You can use it to create a pure function that, say, randomly either adds +1 or
−1.
Randomly add or subtract 1 at each step, starting from 0:
This generates 500 steps in a
“random walk
”:
So far, we
’ve used
NestList iteratively—effectively to perform a chain of applications of a particular function. But you can also use it for
recursion, in which the very pattern of applications of the function is itself nested.
This does a chain of applications of the function f:
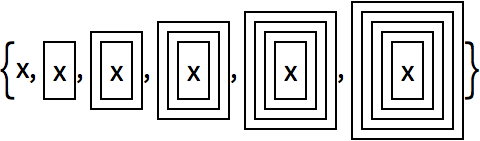
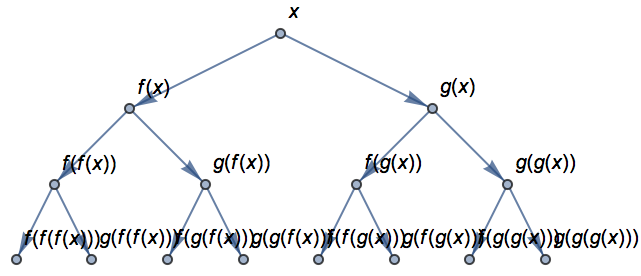
The pattern of applications of f is more complicated here:
Adding frames makes it a little easier to see what
’s going on:
Putting everything in columns shows the nested pattern of function applications.
The nested boxes are recursively combined in twos at each level:
This gives a sequence of recursively nested grids:
This forms the beginning of a fractal structure:
It
’s easy to get some pretty ornate recursive structures:
Not all results from recursion are so complicated. Here
’s an example that successively adds two shifted copies of a list together, as in
{0,1,2,1}+{1,2,1,0}.
Prepend and append 0 to a list, then add together:
If you put the result in a grid, it forms
Pascal’s triangle of
binomial coefficients:
Here
’s another example of recursion with
NestList.
Form a recursive structure with two functions f and g:
Even if things are arranged in columns, it’s still quite difficult to understand the structure that’s been created.
Arrange the recursive structure in columns:
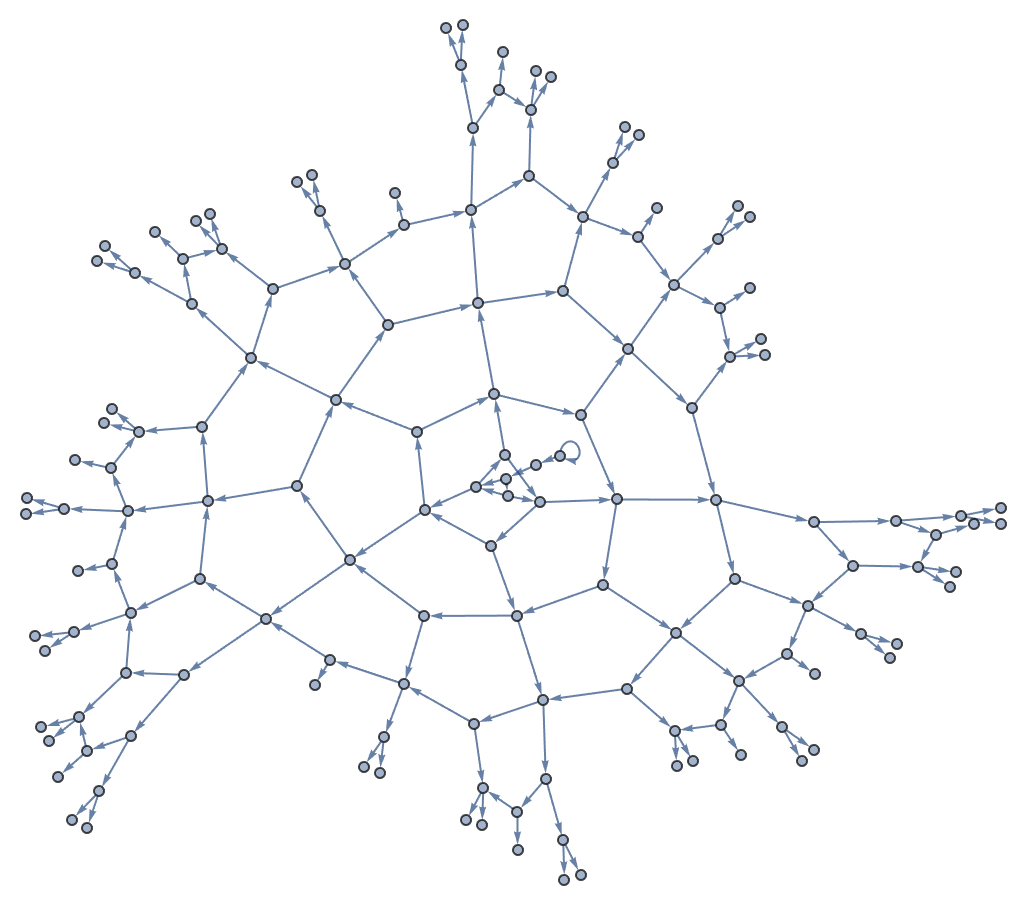
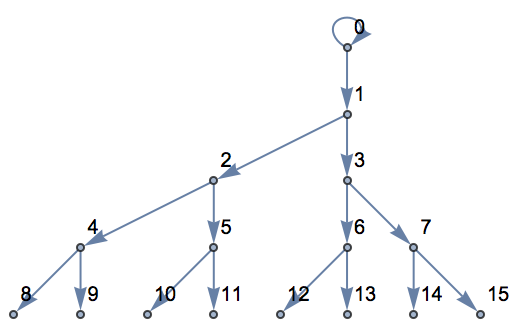
NestGraph is basically like
NestList, except that it makes a graph rather than a list. It repeatedly applies a function to determine what nodes a particular node should connect to. In this case, it produces a tree of nodes, making it clearer what
’s going on.
Start from
x, then repeatedly connect to the list of nodes obtained by applying the function:
Repeatedly apply a numerical function to form another tree structure:
You can use
NestGraph to effectively
“crawl
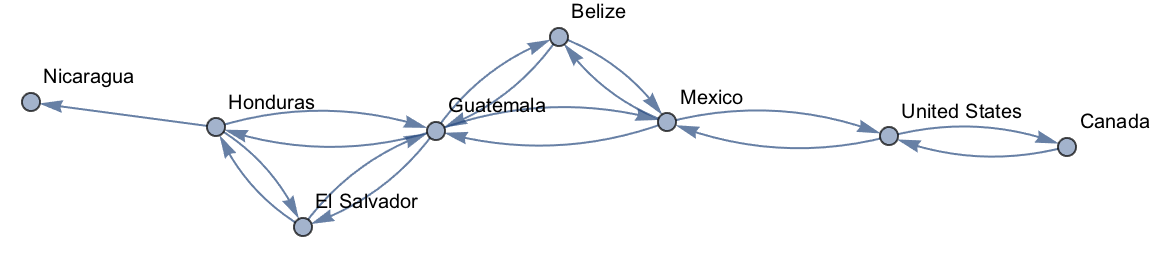
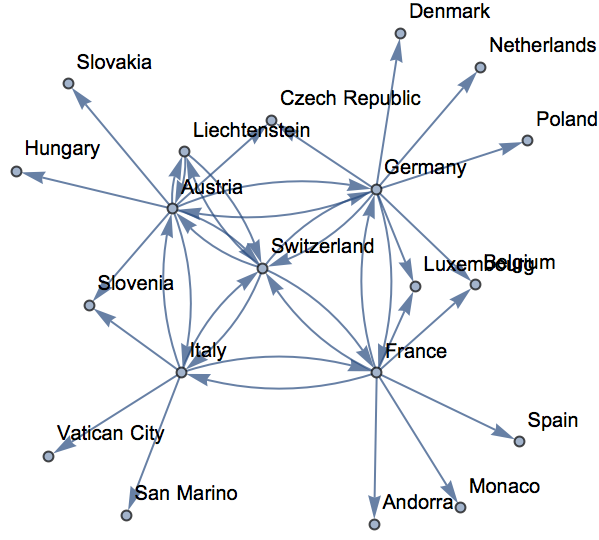
” outward creating a network. As an example, we can repeatedly apply a function that for any country gives a list of countries that border it. The result is a network that connects bordering countries, here starting with Switzerland.
“Crawl” outward 2 steps from Switzerland, connecting each country to all those that border it:
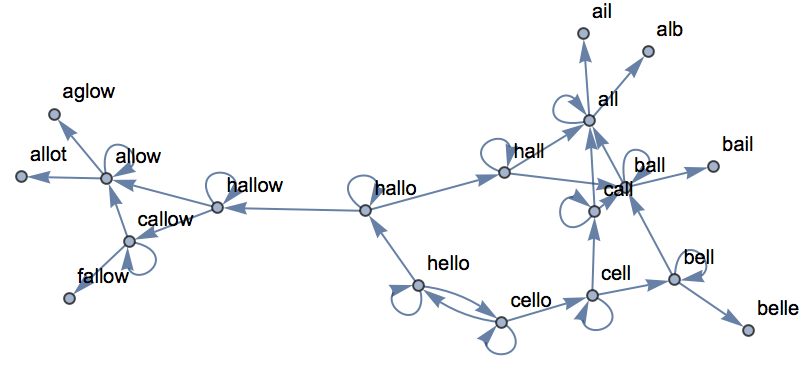
As another example, start from the word
“hello
” and successively connect every word to 3 words in the list of common words that
Nearest considers nearest to it.
Create a network of nearby words with respect to 1-letter changes:
| NestList[f,x,n] | | make a list of applying f to x up to n times |
| Nest[f,x,n] | | give the result of applying f to x exactly n times |
| NestGraph[f,x,n] | | make a graph by nestedly applying f starting with x |
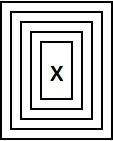
27.1Make a list of the results of nesting
Blur up to 10 times, starting with a rasterized size-30
“X
”.
»
27.2Start with
x, then make a list by nestedly applying
Framed up to 10 times, using a random background color each time.
»
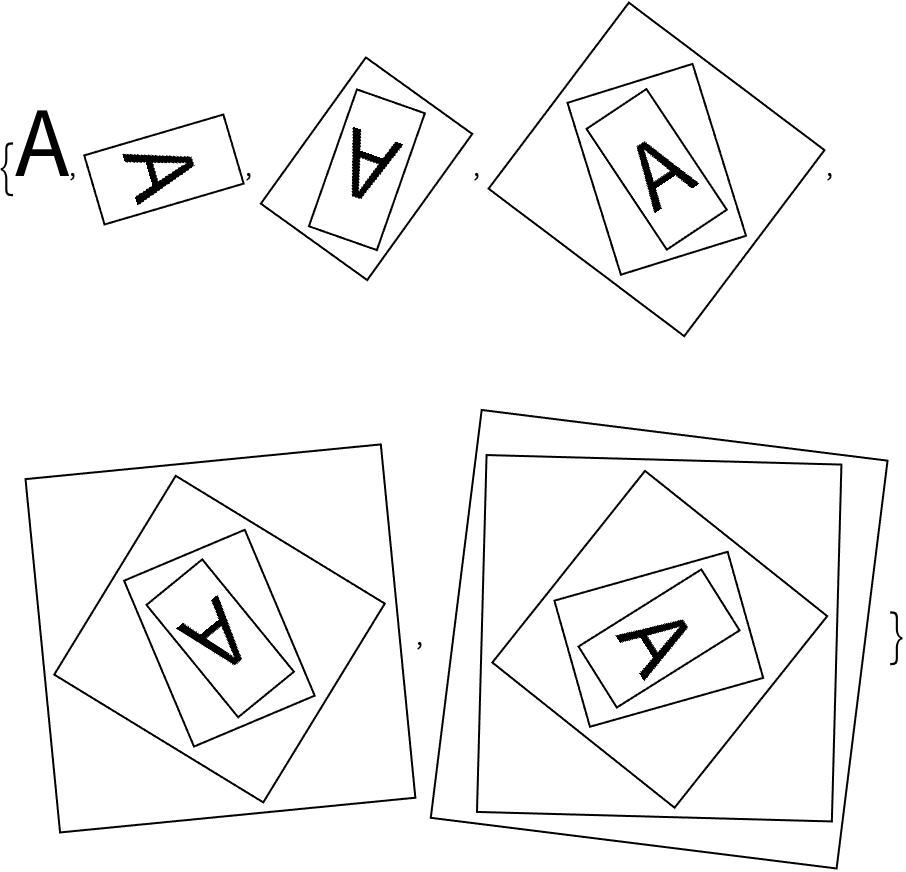
27.3Start with a size-50
“A
”, then make a list of nestedly applying a frame and a random rotation 5 times.
»
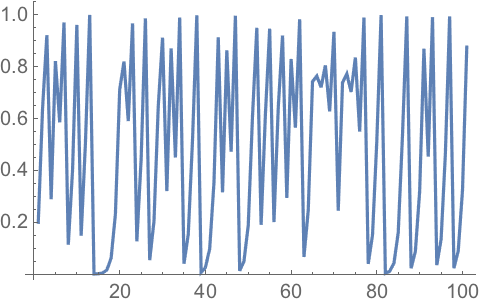
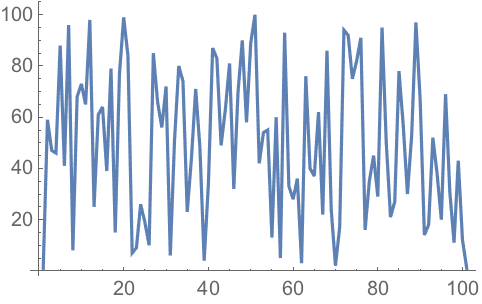
27.4Make a line plot of 100 iterations of the
logistic map iteration 4 #(1-#)&, starting from 0.2.
»
27.5Find the numerical value of the result from 30 iterations of
1+1/#& starting from 1.
»
27.6Create a list of the first 10 powers of 3 (starting at 0) by nested multiplication.
»
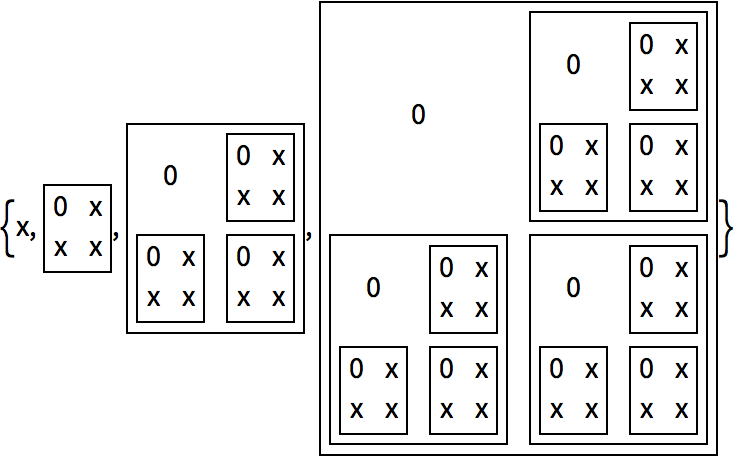
27.7Make a list of the result of nesting the (
Newton’s method) function
(#+2/#)/2& up to 5 times starting from 1.0, and then subtract
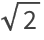
from all the results.
»
27.8Make graphics of a 1000-step 2D random walk which starts at
{0, 0}, and in which at each step a pair of random numbers between
−1 and +1 are added to the coordinates.
»
27.9Make an array plot of 50 steps of Pascal
’s triangle modulo 2 by starting from
{1} and nestedly joining
{0} at the beginning and at the end, and adding these results together modulo 2.
»
27.10Generate a graph by starting from 0, then nestedly 10 times connecting each node with value
n to ones with values
n+1 and
2n.
»
27.11Generate a graph obtained by nestedly finding bordering countries starting from the United States, and going 4 iterations.
»
+27.1Make a line plot of 100 iterations of
linear congruential function Mod[59#, 101]&, starting from 1.
»
+27.2Create a list of 5
power towers of 2, i.e.
2^2^2...^2 n times, with
n from 0 to 4.
»
+27.3Create a list of 20
power towers of 1.2, i.e.
1.2^1.2^...^1.2 n times, with
n from 0 to 19.
»
+27.4Generate a list of the numerical values obtained by up to 10 nestings of the function
Sqrt[1+#]&.
»
+27.5Make graphics of a 1000-step 3D random walk which starts at
{0, 0, 0}, and in which at each step a triple of random numbers between
−1 and +1 are added to the coordinates.
»
What’s the difference between iteration and recursion?
If one does one thing repeatedly, it
’s iteration. When one takes the result of an operation and applies the same operation to it wherever it is, that
’s recursion. It
’s slightly confusing, because simple cases of recursion are just iteration.
NestList always does recursion, but if only one slot appears in the function, the recursion can be
“unrolled
” into iteration.
What is the relation between nesting, recursion and fractals?
They are very closely related. The definitions aren
’t precise, but fractals are basically geometrical forms that exhibit some type of nested or recursive structure.
What is Pascal’s triangle?
It
’s a very common structure discussed in elementary mathematics. Its definition is very close to the Wolfram Language code here: at each row each number is computed as the sum of the numbers directly above it and above it to its right. Each row gives the coefficients in the expansion of
(1+x)^n.
Conceptually yes. One can think of it as doing the analog of starting from a webpage and then visiting links from that page, and continuing recursively with that process. We
’ll see an example of this in
Section 44.
Why do some but not all countries have arrows both ways in the bordering countries graph?
If
NestGraph was run for enough steps, all countries would have arrows both ways, since if A borders B, then B borders A. But here we
’re stopping after just 2 steps, so many of the reverse connections haven
’t been reached.
You don
’t need to. You can just use
Power, as in
Table[2^n, {n, 0, 15}]. But it
’s nice to see the sequence
Plus,
Times,
Power arise from successive nesting (e.g.
NestList[2+#&, 0, 15] is
Table[2*n, {n, 0, 15}]).
Is there a way to keep applying a function until nothing is changing?
- The nearest words example can be made much more efficient by first computing a NearestFunction, then using this repeatedly, rather than computing Nearest from scratch for every word. This example is also closely related to NearestNeighborGraph, discussed in Section 22.

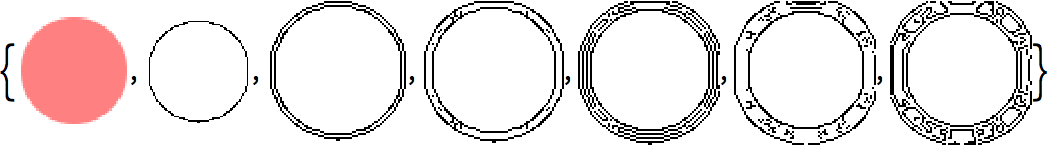
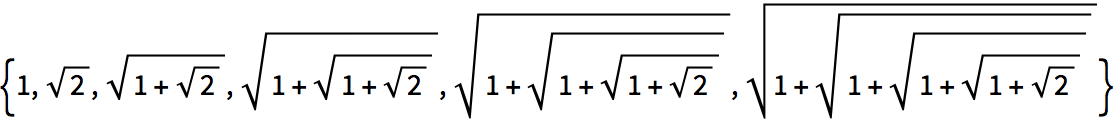
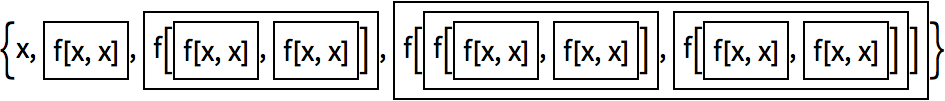
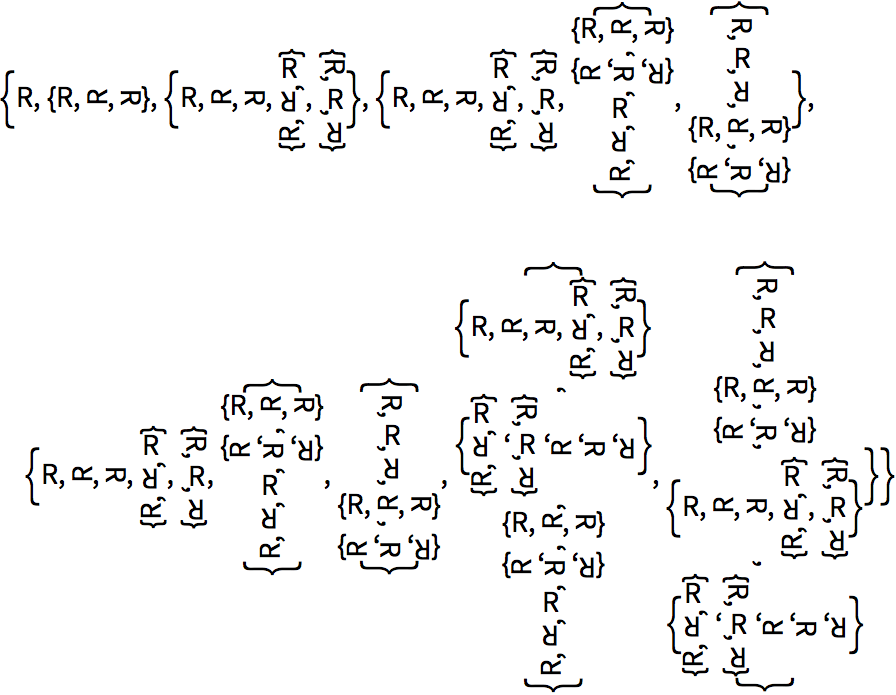

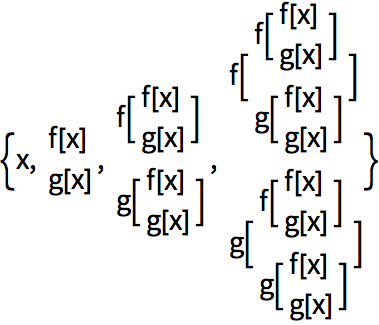
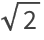 from all the results. »
from all the results. »