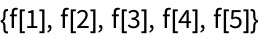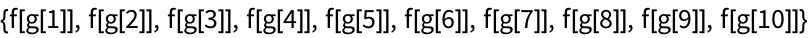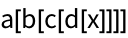WOLFRAM

Explore the latest version of An Elementary Introduction to the Wolfram Language »
Stephen Wolfram
An Elementary Introduction to the Wolfram Language
Second Edition (2017)
25Ways to Apply Functions
When you write f[x] it means “apply the function f to x”. An alternative way to write the same thing in the Wolfram Language is f@x.
f@x is the same as f[x]:
In[1]:=
Click for copyable input
Out[1]=
It’s often convenient to write out chains of functions using @:
In[2]:=
Click for copyable input
Out[2]=
Avoiding the brackets can make code easier to type, and read:
In[3]:=
Click for copyable input
Out[3]=
There’s a third way to write f[x] in the Wolfram Language: as an “afterthought”, in the form x//f.
Apply f “as an afterthought” to x:
In[4]:=
Click for copyable input
Out[4]=
You can have a sequence of “afterthoughts”:
In[5]:=
Click for copyable input
Out[5]=
The functions here read in the order they are applied:
In[6]:=
Click for copyable input
Out[6]=
A particularly common use of // is to apply N (for numerical evaluation) “as an afterthought”.
Apply numerical evaluation “as an afterthought”:
In[7]:=
Click for copyable input
Out[7]=
In working with the Wolfram Language, a powerful notation that one ends up using all the time is /@, which means “apply to each element”.
Apply f to each element in a list:
In[8]:=
Click for copyable input
Out[8]=
f usually would just get applied to the whole list:
In[9]:=
Click for copyable input
Out[9]=
Framed is a function that displays a frame around something.
Display x framed:
In[10]:=
Click for copyable input
Out[10]=
Applying Framed to a list just puts a frame around the whole list.
Apply Framed to a whole list:
In[11]:=
Click for copyable input
Out[11]=
@ does exactly the same thing:
In[12]:=
Click for copyable input
Out[12]=
Now use /@ to apply Framed to each element in the list:
In[13]:=
Click for copyable input
Out[13]=
The same thing works with any other function. For example, apply the function Hue separately to each number in a list.
/@ applies Hue separately to each number in the list:
In[14]:=
Click for copyable input
Out[14]=
Here’s what the /@ is doing:
In[15]:=
Click for copyable input
Out[15]=
It’s the same story with Range, though now the output is a list of lists.
/@ applies Range separately to each number, producing a list of lists:
In[16]:=
Click for copyable input
Out[16]=
Here’s the equivalent, all written out:
In[17]:=
Click for copyable input
Out[17]=
Given a list of lists, /@ is what one needs to do an operation separately to each sublist.
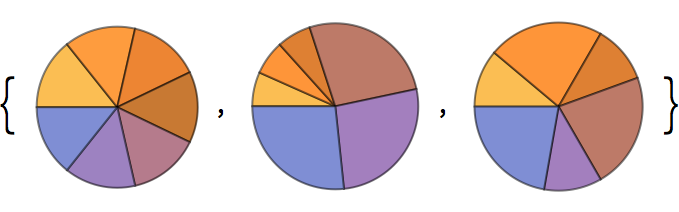
Apply PieChart separately to each list in a list of lists:
In[18]:=
Click for copyable input
Out[18]=
You can use exactly the same idea with lots of other functions.
Apply Length to each element, getting the length of each sublist:
In[19]:=
Click for copyable input
Out[19]=
Applying Length to the whole list just gives the total number of sublists:
In[20]:=
Click for copyable input
Out[20]=
Apply Reverse to each element, getting three different reversed lists:
In[21]:=
Click for copyable input
Out[21]=
Apply Reverse to the whole list, reversing its elements:
In[22]:=
Click for copyable input
Out[22]=
As always, the form with brackets is exactly equivalent:
In[23]:=
Click for copyable input
Out[23]=
Some calculational functions are listable, which means they automatically apply themselves to elements in a list.
N is listable, so you don’t have to use /@ to get it applied to each element in a list:
In[24]:=
Click for copyable input
Out[24]=
The same is true with Prime:
In[25]:=
Click for copyable input
Out[25]=
A function like Graphics definitely isn’t listable.
This makes a single graphic with three objects in it:
In[26]:=
Click for copyable input
Out[26]=
This gives three separate graphics, with Graphics applied to each object:
In[27]:=
Click for copyable input
Out[27]=
When you enter f/@{1,2,3}, the Wolfram Language interprets it as Map[f,{1,2,3}]. f/@x is usually read as “map f over x”.
The internal interpretation of f/@{1, 2, 3}:
In[28]:=
Click for copyable input
Out[28]=
Vocabulary
f@x equivalent to f[x]
x//f equivalent to f[x]
f/@{a,b,c} apply f separately to each element of the list
Map[f,{a,b,c}] alternative form of /@
Framed[expr] put a frame around something
25.1Use /@ and Range to reproduce the result of Table[f[n], {n, 5}]. »
Expected output:
Out[]=
25.2Use /@ twice to generate Table[f[g[n]], {n, 10}]. »
Expected output:
Out[]=
25.3Use // to create a[b[c[d[x]]]]. »
Expected output:
Out[]=
Expected output:
Out[]=
Expected output:
Out[]=
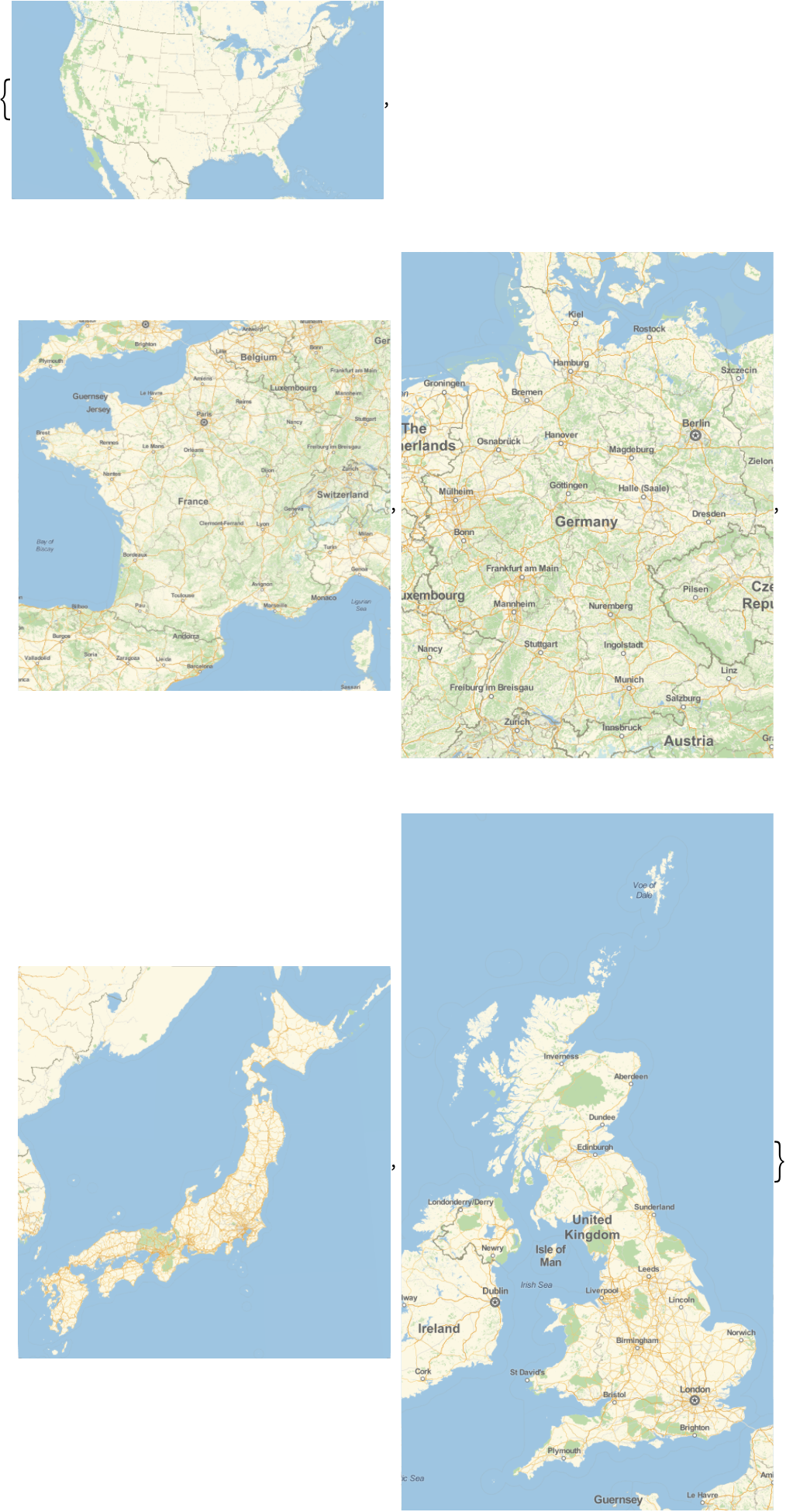
25.6Use /@ to draw separate maps of each country in the G5. »
Expected output:
Out[]=
25.7Binarize each flag in Europe, and make an image collage of the result. »
Expected output:
Out[]=
25.8Find a list of the dominant colors in images of the planets, putting the results for each planet in a column. »
Expected output:
Out[]=
25.9Find the total of the letter numbers given by LetterNumber for the letters in the word “wolfram”. »
Expected output:
Out[]=
Q&A
Why not always use f@x instead of f[x]?
f@x is a fine equivalent to f[x], but the equivalent of f[1+1] is f@(1+1), and in that case, f[1+1] is shorter and easier to understand.
Why is /@ called Map?
It comes from math. Given a set {1, 2, 3}, f/@{1, 2, 3} can be thought of as mapping of this set to another one.
How does one say "//" and "/@"?
Typically “slash slash” and “slash at”.
When do I need to use parentheses with @, // and /@?
It’s determined by the precedence or binding of different operators. @ binds tighter than +, so f@1+1 means f[1]+1 not f@(1+1) or f[1+1]. // binds looser than +, so 1/2+1/3//N means (1/2+1/3)//N. In a notebook you can find how things are grouped by repeatedly clicking on your input, and seeing how the selection expands.
Tech Notes
More to Explore
Guide to Functional Programming in the Wolfram Language »
 
Download Notebook Version
es