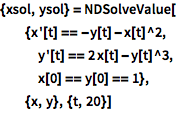Wolfram Language Fast Introduction for Math Students
Get Started »

Differential Equations

The Wolfram Language can find solutions to ordinary, partial and delay differential equations (ODEs, PDEs and DDEs).

DSolveValue takes a differential equation and returns the general solution:

(C[1] stands for a constant of integration.)
In[1]:=
Click for copyable input
⨯ 
sol = DSolveValue[y'[x] + y[x] == x, y[x], x]
Out[1]=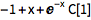

Use /. to replace the constant:

In[2]:=
Click for copyable input
⨯ 
sol /. C[1] -> 1
Out[2]=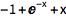

Or add conditions for a specific solution:

In[3]:=
Click for copyable input
⨯ 
DSolveValue[{y'[x] + y[x] == x, y[0] == -1}, y[x], x]
Out[3]=

NDSolveValue finds numerical solutions:

In[1]:=
Click for copyable input
⨯ 
NDSolveValue[{y'[x] == Cos[x^2], y[0] == 0}, y[x], {x, -5, 5}]
Out[1]=

You can plot this InterpolatingFunction directly:

In[2]:=
Click for copyable input
⨯ 
Plot[%, {x, -5, 5}]
Out[2]=

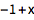To solve systems of differential equations, include all equations and conditions in a list:

(Note that the line breaks have no effect.)
In[1]:=
Click for copyable input
⨯ 
{xsol, ysol} = NDSolveValue[
  {x'[t] == -y[t] - x[t]^2,
   y'[t] == 2 x[t] - y[t]^3,
   x[0] == y[0] == 1},
  {x, y}, {t, 20}]
Out[1]=

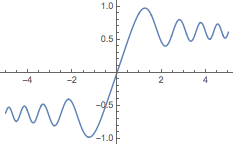
Visualize the solution as a parametric plot:

In[2]:=
Click for copyable input
⨯ 
ParametricPlot[{xsol[t], ysol[t]}, {t, 0, 20}]
Out[2]=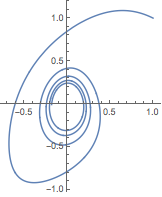

QUICK REFERENCE: Differential Equations »