Sequences, Sums & Series
In the Wolfram Language, integer sequences are represented by lists.
Use Table to define a simple sequence:
| Out[1]= | 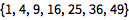 |
Some well-known sequences are built in:
| Out[2]= | 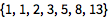 |
Define a recursive sequence using RecurrenceTable:
(Note the use of {x,min,max} notation.)
| Out[1]= | 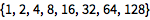 |
Compute the Total of the sequence:
| Out[2]= | 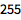 |
Compute the Sum of a sequence from its generating function:
Use ESCsumtESC for a fillable typeset form:
You can do indefinite and multiple sums:
Generate power series approximations to virtually any combination of built-in functions:
O[x]9 represents higher-order terms that have been omitted; use Normal to truncate this term:
Given an unknown or undefined function, Series returns a power series in terms of derivatives:
