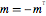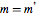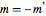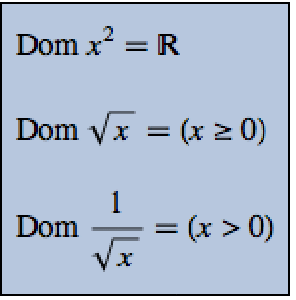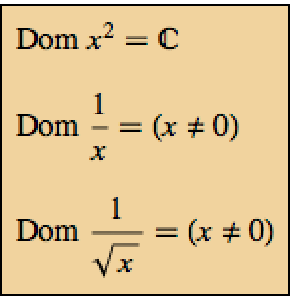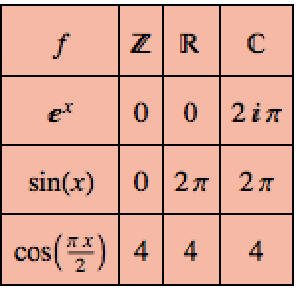Matrix-Prädikate
Mathematica 10 führt eine Reihe von Matrix-Prädikaten zum Testen von Matrixeigenschaften ein. Matrix-Prädikate werden normalerweise für Algorithmen verwendet, die eine Eigenschaft von Eingabe-Matritzen überprüfen, bevor der Algorithmus ausgeführt wird.
Symmetriebezogene Matrix-Prädikate.
Matrix-Prädikate in quadratischer Form.
| PositiveDefiniteMatrixQ[m] | 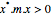 for all nonzero for all nonzero 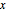 | |
| PositiveSemidefiniteMatrixQ[m] | 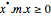 for all nonzero for all nonzero 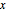 | |
| NegativeDefiniteMatrixQ[m] | 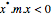 for all nonzero for all nonzero 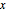 | |
| NegativeSemidefiniteMatrixQ[m] | 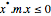 for all nonzero for all nonzero 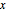 | |
| IndefiniteMatrixQ[m] | otherwise |
Skalarproduktbezogene Matrix-Prädikate.
| OrthogonalMatrixQ[m] | 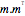 is identity matrix, is identity matrix, 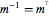 | |
| UnitaryMatrixQ[m] | 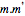 is identity matrix, is identity matrix, 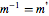 |
Eigenwertbezogene Matrix-Prädikate.
| DiagonalizableMatrixQ[m] | 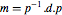 for diagonal for diagonal | |
| NormalMatrixQ[m] | 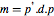 for diagonal for diagonal 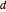 or or 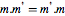 |