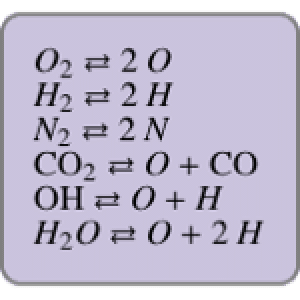Solve Geometric Problems as Polynomial Systems 

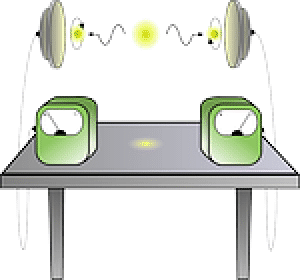
Find the diameter of a solid in 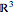given by a polynomial inequality.

In[1]:=

X f[x_, y_, z_] := x^4 - 5 x^2 y z + 3 x^2 y^2 + 10 x^2 y z + 3 x^2 y^2 - y^3 z + y^4 + z^4 - 1; f[x, y, z] <= 0

Out[1]=

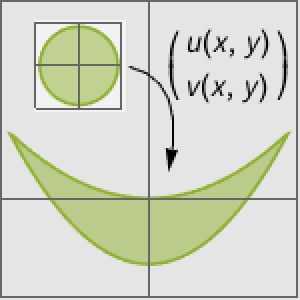
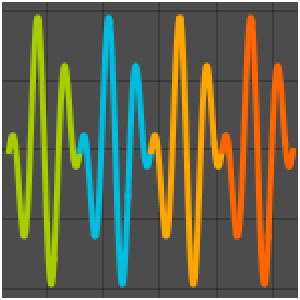
Visualize the region.

In[2]:=

X RegionPlot3D[ f[x, y, z] <= 0, {x, -1.5, 1.5}, {y, -1.5, 1.5}, {z, -1.5, 1.5}, PlotPoints -> 50, PlotTheme -> {"Scientific", "NoMesh"}]

Out[2]=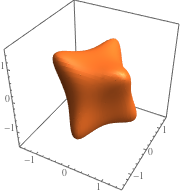

Formulate a necessary condition for a local maximum of the distance between two points on the boundary of ℛ.

In[3]:=

X grad[x_, y_, z_] := Grad[f[x, y, z], {x, y, z}] p = {p1, p2, p3}; q = {q1, q2, q3}; cond = f @@ p == 0 && f @@ q == 0 && And @@ Thread[grad @@ p == \[Lambda] (p - q)] && And @@ Thread[grad @@ q == \[Mu] (p - q)]

Out[3]=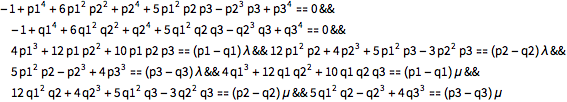

Use NSolve to find pairs 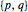satisfying the condition.

In[4]:=

X sols = NSolve[\!\( \*SubscriptBox[\(\[Exists]\), \({\[Lambda], \[Mu]}\)]cond\), Join[p, q], Reals];

Find the diameter of ℛ.

In[5]:=

X diam = Max[Norm[p - q] /. sols]

Out[5]=

Find the distinct pairs 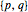realizing the maximum distance.

In[6]:=

X pairs = Union[Select[{p, q} /. sols, Norm[Subtract @@ #] == diam &], SameTest -> (Max[Sort[#1] - Sort[#2]] < 10^-9 &)]

Out[6]=

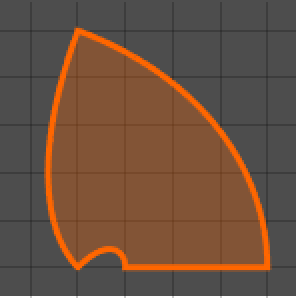
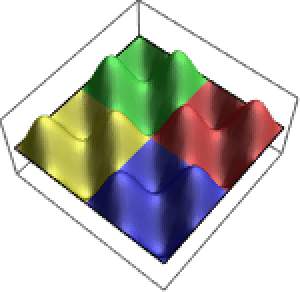
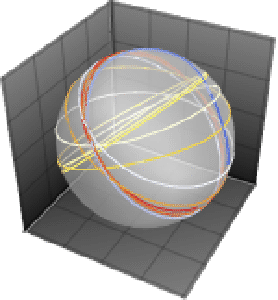
Visualize the result.

show complete Wolfram Language inputhide input

In[7]:=

X Show[{RegionPlot3D[ f[x, y, z] <= 0, {x, -1.5, 1.5}, {y, -1.5, 1.5}, {z, -1.5, 1.5}, PlotPoints -> 50, PlotStyle -> Opacity[0.6], PlotTheme -> {"Scientific", "NoMesh"}], Graphics3D[{{Cyan, Sphere[#, .1]}, {Black, Thick, Line[#]}} & /@ pairs]}]

Out[7]=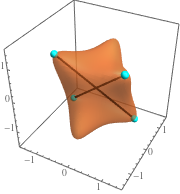