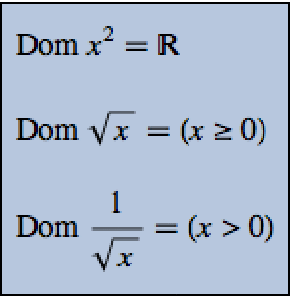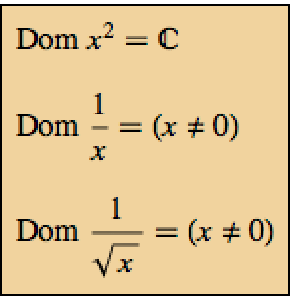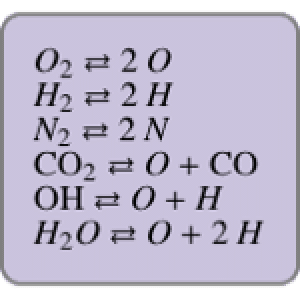Find Chemical Equilibrium for Networks of Reactions 

Chemical reaction systems that have equilibrium can typically be directly modeled as a polynomial system of equations. These problems are defined by conservation and reaction equations. The example below is from combustion chemistry and models the burning of fuel in a combustion chamber such as in a car engine. The goal is to find out what chemical components and compounds are in the combustion chamber at various stages. The system of reactions being studied is given by , , , , , , .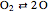

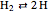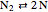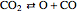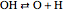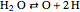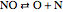Introduce a variable for the quantity of each component. Here 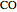is treated as a component, since 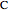does not occur on its own.

Also introduce a variable for the quantity of each compound.

In[1]:=

X vars = {Subscript[x, 1], Subscript[x, 2], Subscript[x, 3], Subscript[ x, 4], Subscript[x, 5], Subscript[x, 6], Subscript[x, 7], Subscript[x, 8], Subscript[x, 9], Subscript[x, 10]};

If you assume a closed chemical system, quantities are conserved, which leads to conservation equations shown in their chemical and algebraic notation.

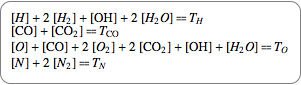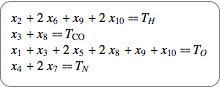In[2]:=

X conservation = {Subscript[x, 2] + 2 Subscript[x, 6] + Subscript[x, 9] + 2 Subscript[x, 10] == Subscript[T, H], Subscript[x, 3] + Subscript[x, 8] == Subscript[T, CO], Subscript[x, 1] + Subscript[x, 3] + 2 Subscript[x, 5] + 2 Subscript[x, 8] + Subscript[x, 9] + Subscript[x, 10] == Subscript[T, O], Subscript[x, 4] + 2 Subscript[x, 7] == Subscript[T, N]};

Give the equations for equilibrium.

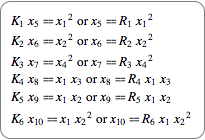In[3]:=

X equilibrium = {Subscript[x, 5] == Subscript[R, 1] Subscript[x, 1]^2, Subscript[x, 6] == Subscript[R, 2] Subscript[x, 2]^2, Subscript[x, 7] == Subscript[R, 3] Subscript[x, 4]^2, Subscript[x, 8] == Subscript[R, 4] Subscript[x, 1] Subscript[x, 3], Subscript[x, 9] == Subscript[R, 5] Subscript[x, 1] Subscript[x, 2], Subscript[x, 10] == Subscript[R, 6] Subscript[x, 1] Subscript[x, 2]^2};

Give parameter values.

In[4]:=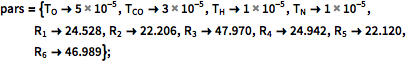

X pars = {Subscript[T, O] -> 5 10^-5, Subscript[T, CO] -> 3 10^-5, Subscript[T, H] -> 1 10^-5, Subscript[T, N] -> 1 10^-5, Subscript[R, 1] -> 24.528, Subscript[R, 2] -> 22.206, Subscript[R, 3] -> 47.970, Subscript[R, 4] -> 24.942, Subscript[R, 5] -> 22.120, Subscript[R, 6] -> 46.989};

Solve the system over the reals, and select only non-negative solutions.

In[5]:=

X rsols = NSolve[Join[conservation, equilibrium] /. pars, vars, Reals];

In[6]:=

X Thread[vars -> SelectFirst[vars /. rsols, VectorQ[#, NonNegative] &]]

Out[6]=

Compute a higher-precision solution.

In[7]:=

X rsols = NSolve[ SetPrecision[Join[conservation, equilibrium] /. pars, 20], vars, Reals, WorkingPrecision -> 20];

In[8]:=

X Thread[vars -> SelectFirst[vars /. rsols, VectorQ[#, NonNegative] &]]

Out[8]=