Observe a Quantum Particle in a Box: New in Wolfram Language 11

Observe a Quantum Particle in a Box

A quantum particle free to move within a two-dimensional rectangle with sides 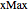and 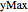is described by the two-dimensional time-dependent Schrödinger equation, together with boundary conditions that force the wavefunction to zero at the boundary.

In[1]:=

eqn = I D[\[Psi][x, y, t], t] == -\[HBar]^2/(2 m)
     Laplacian[\[Psi][x, y, t], {x, y}];

In[2]:=

bcs = {\[Psi][0, y, t] == 0, \[Psi][xMax, y, t] == 
    0, \[Psi][x, yMax, t] == 0, \[Psi][x, 0, t] == 0};

This equation has a general solution that is a formal infinite sum of so-called eigenstates.

In[3]:=

DSolveValue[{eqn, bcs}, \[Psi][x, y, t], {x, y, t}]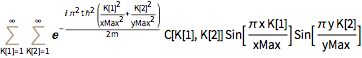

Out[3]=

Define an initial condition equal to a unitized eigenstate.

In[4]:=

initEigen = \[Psi][x, y, 0] == 
   2 /Sqrt[xMax yMax] Sin[(\[Pi] x)/xMax] Sin[(\[Pi] y)/yMax];

In this case, the solution is simply a time-dependent multiple (of unit modulus) of the initial condition.

In[5]:=

DSolveValue[{eqn, bcs, initEigen}, \[Psi][x, y, t], {x, y, t}]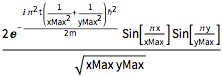

Out[5]=

Define an initial condition that is a sum of eigenstates. Because the initial conditions are not an eigenstate, the probability density for the location of the particle will be time dependent.

In[6]:=

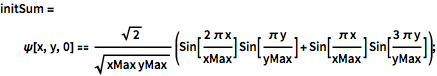
initSum = \[Psi][x, y, 0] == 
   Sqrt[2]/Sqrt[
    xMax yMax] (Sin[(2 \[Pi] x)/xMax] Sin[(\[Pi] y)/yMax] + 
      Sin[(\[Pi] x)/xMax] Sin[(3 \[Pi] y)/yMax]);

Solve with the new initial condition.

In[7]:=

sol = DSolveValue[{eqn, bcs, initSum}, \[Psi][x, y, t], {x, y, t}]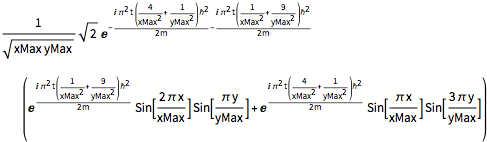

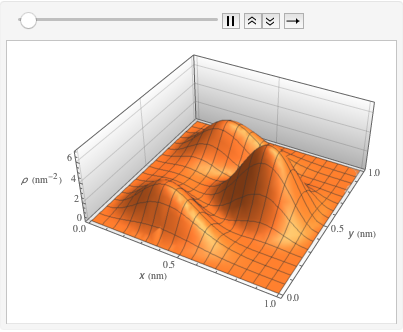
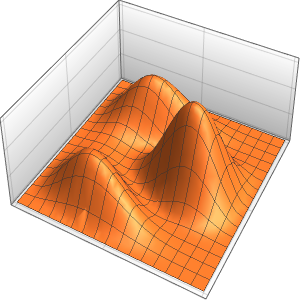
Out[7]=

Compute the probability density, inserting values of the reduced Planck's constant, electron mass, and a box of atomic size, using units of the electron mass, nanometers, and femtoseconds.

In[8]:=

\[HBar] = 
 QuantityMagnitude[Quantity[1., "ReducedPlanckConstant"], 
  "ElectronMass" * ("Nanometers")^2/"Femtoseconds"]

Out[8]=

In[9]:=

\[Rho][x_, y_, t_] = 
 FullSimplify[ComplexExpand[Conjugate[sol] sol]] /. {m -> 1, 
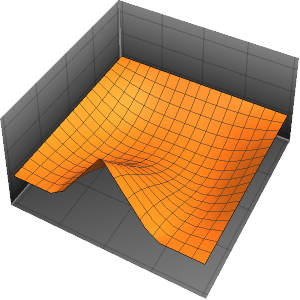
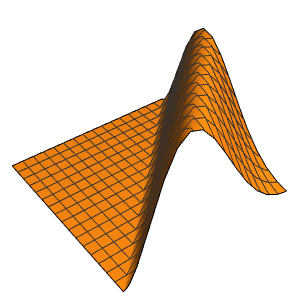
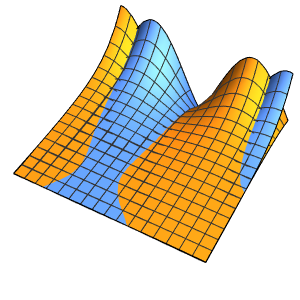
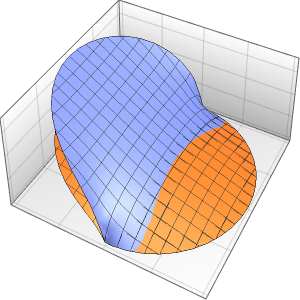
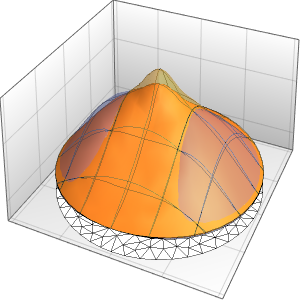
   xMax -> 1, yMax -> 1}

Out[9]=

Visualize the probability density inside the box over time.

In[10]:=

ListAnimate[
 Table[Plot3D[\[Rho][x , y , t], {x, 0, 1}, {y, 0, 1}, 
   PlotTheme -> {"Scientific", "SolidGrid"}, AxesLabel -> {"\!\(\*
StyleBox[\"x\", \"SO\"]\) (nm)", " \!\(\*
StyleBox[\"y\", \"SO\"]\) (nm)", "\!\(\*
StyleBox[\"\[Rho]\", \"SO\"]\) (\!\(\*SuperscriptBox[\(nm\), \
\(-2\)]\))"}, ImageSize -> Medium, PlotRange -> {0, 7}], {t, 0, 
   19, .5}]]