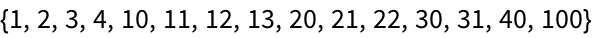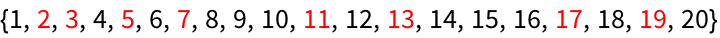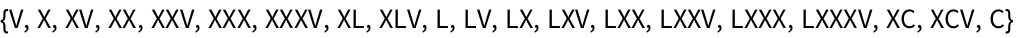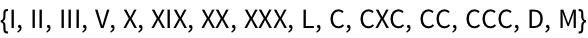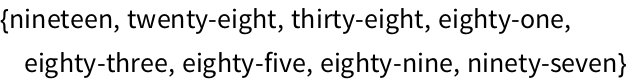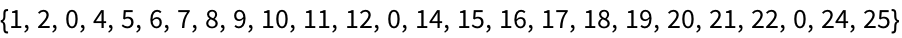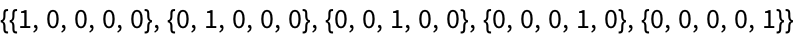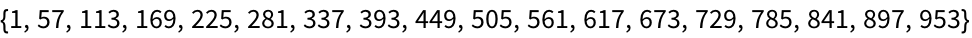Is 2+2 equal to 4? Let
’s ask the Wolfram Language.
Test whether 2+2 is equal to 4:
Not surprisingly, testing whether 2+2 is equal to 4 gives
True.
We can also test whether 2
×2 is greater than 5. We do that using
>.
Test whether 2
×2 is greater than 5:
The function
If lets you choose to give one result if a test is
True, and another if it
’s
False.
Since the test gives
True, the result of the
If is
x:
By using a pure function with
/@, we can apply an
If to every element of a list.
If an element is less than 4, make it x, otherwise make it y:
You can also test for less than or equal using
≤, which is typed as
<=.
If an element is less than or equal to 4, make it x; otherwise, make it y:
This makes an element x only if it is equal to 4:
You can test whether two things are not equal using
≠, which is typed as
!=.
If an element is not equal to 4, make it x; otherwise, make it y:
It
’s often useful to select elements in a list that satisfy a test. You can do this by using
Select, and giving your test as a pure function.
Select elements in the list that are greater than 3:
Select elements that are between 2 and 5:
Beyond size comparisons like
<,
> and
==, the Wolfram Language includes many other kinds of tests. Examples are
EvenQ and
OddQ, which test whether numbers are even or odd. (The
“Q” indicates that the functions are asking a question.)
4 is an even number:
Select even numbers from the list:
In this case, we don’t need the explicit pure function:
IntegerQ tests whether something is an integer;
PrimeQ tests whether a number is prime.
Select prime numbers:
Sometimes we need to combine tests.
&& represents
“and
”,
|| represents
“or
” and
! represents
“not
”.
Select elements of the list that are both even and greater than 2:
Select elements that are either even or greater than 4:
Select elements that are not either even or greater than 4:
There are many other
“Q functions
” that ask various kinds of questions.
LetterQ tests whether a string consists of letters.
The space between letters isn’t a letter; nor is “!”:
Turn a string into a list of characters, then test which are letters:
Select the characters that are letters:
Select letters that appear after position 10 in the alphabet:
You can use
Select to find words in English that are
palindromes, meaning that they are the same if you reverse them.
MemberQ tests whether something appears as an element, or member, of a list.
5 appears in the list {1, 3, 5, 7}:
Select numbers in the range 1 to 100 whose digit sequences contain 2:
ImageInstanceQ is a machine-learning-based function that tests whether an image is an instance of a particular kind of thing, like a cat.
Test if an image is of a cat:
Select images of cats:
Here
’s a geographic example of
Select: find which cities in a list are less than 3000 miles from San Francisco.
Select cities whose distance from San Francisco is less than 3000 miles:
| ab | | test for equality |
| a<b | | test whether less |
| a>b | | test whether greater |
| a≤b | | test whether less or equal |
| a≥b | | test whether greater or equal |
| If[test,u,v] | | give u if test is True and v if False |
| Select[list,f] | | select elements that pass a test |
| EvenQ[x] | | test whether even |
| OddQ[x] | | test whether odd |
| IntegerQ[x] | | test whether an integer |
| PrimeQ[x] | | test whether a prime number |
| LetterQ[string] | | test whether there are only letters |
| MemberQ[list,x] | | test whether x is a member of list |
| ImageInstanceQ[image,category] | | test whether image is an instance of category |
28.1Test whether 123^321 is greater than 456^123.
»
28.2Get a list of numbers up to 100 whose digits add up to less than 5.
»
28.3Make a list of the first 20 integers, with prime numbers styled red.
»
28.4Find words in
WordList[ ] that both begin and end with the letter
“p
”.
»
28.5Make a list of the first 100 primes, keeping only ones whose last digit is less than 3.
»
28.6Find Roman numerals up to 100 that do not contain
“I
”.
»
28.7Get a list of Roman numerals up to 1000 that are palindromes.
»
28.8Find names of integers up to 100 that begin and end with the same letter.
»
28.9Get a list of words longer than 15 characters from the Wikipedia article on words.
»
28.10Starting from 1000, divide by 2 if the number is even, and compute
3#+1& if the number is odd; do this repeatedly 200 times (
Collatz problem).
»
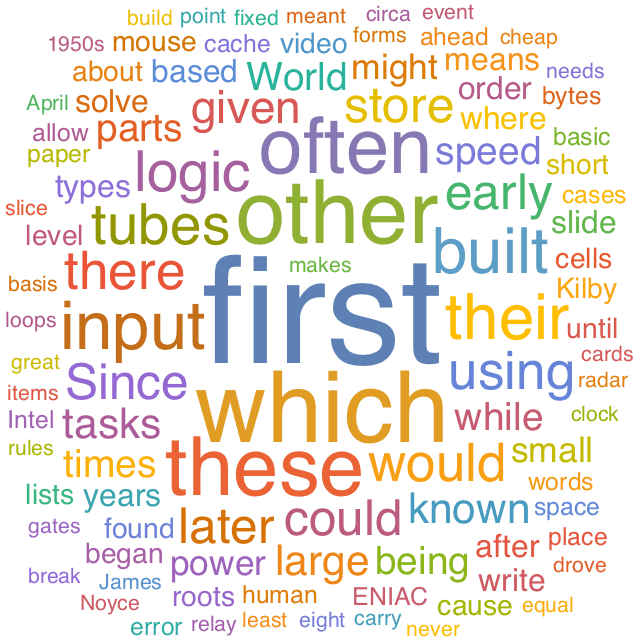
28.11Make a word cloud of 5-letter words in the Wikipedia article on computers.
»
28.12Find words in
WordList[ ] whose first 3 letters are the same as their last 3 read backward, but where the whole string is not a palindrome.
»
+28.1Make a table of integers up to 25 where every integer ending in 3 is replaced with 0.
»
+28.2Use
Table and
If to make a 5
×5 array that is 1 on its leading diagonal, and 0 otherwise.
»
+28.3Get a list of numbers up to 1000 that are equal to 1 mod both 7 and 8.
»
+28.4Make a list of numbers up to 100, where multiples of 3 are replaced by
Black, multiples of 5 by
White and multiples of 3 and 5 by
Red.
»
+28.5Use
Select to get a list of planets whose mass is larger than Earth.
»
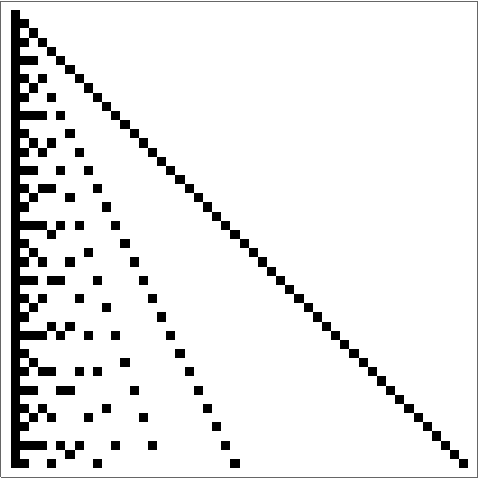
+28.6Make a 50
×50 array plot in which a square at position
i, j is black if
Mod[i, j]==0.
»
+28.7Make a 100
×100 array plot in which a square is black if the values of both its
x and
y positions do not contain a 5.
»
Why does one test equality with
== not
=?
Because
= means something else in the Wolfram Language. You
’ll get very strange results if you use
= instead of
== by mistake. (
= is for assigning values of variables.) To avoid possible confusion,
== is often read as
“double equals
”.
Why is
“and
” written as
&&, not
&?
Because
& means other things in the Wolfram Language. For example it
’s what ends a pure function.
How are
==,
>,
&&, etc. interpreted?
When do I need to use parentheses with
&&,
||, etc.?
There
’s an order of operations that
’s a direct analog of arithmetic.
&& is like
×,
|| is like
+, and
! is like
−. So
!p&&q means
“(not
p) and
q”;
!(p&&q) means
“not (
p and
q)
”.
What
’s special about
“Q” functions?
They ask a question that normally has an answer of
True or
False.
What are some other
“Q
” functions?
Is there a better way to find real-world entities with certain properties than using
Select?
Yes. You can do things like
Entity["Country", "Population"GreaterThan[]] to find
“implicit entities
”, then use
EntityList to get explicit lists of entities.
- True and False are typically called Booleans in computer science, after George Boole from the mid-1800s. Expressions with &&, ||, etc. are often called Boolean expressions.
- In the Wolfram Language, True and False are symbols, and are not represented by 1 and 0 as in many other computer languages.
- If is often called a conditional. In If[test, then, else], the then and else aren’t computed unless the test says their condition is met.
- PalindromeQ directly tests if a string is a palindrome.
- In the Wolfram Language, x is a symbol (see Section 33) that could represent anything, so x==1 is just an equation, that isn’t immediately True or False. x===1 (“triple equals”) tests whether x is the same as 1, and since it isn’t, it gives False.