영구식을 사용한 조합 문제 해결

영구식은 행렬식과 비슷하지만, 모든 항목의 부호가 플러스 부호임이 다른점입니다.

In[1]:=

Permanent[\!\(\* TagBox[ RowBox[{"(", "", GridBox[{ { SubscriptBox["a", RowBox[{"1", ",", "1"}]], SubscriptBox["a", RowBox[{"1", ",", "2"}]]}, { SubscriptBox["a", RowBox[{"2", ",", "1"}]], SubscriptBox["a", RowBox[{"2", ",", "2"}]]} }, GridBoxAlignment->{ "Columns" -> {{Left}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}, "Items" -> {}, "ItemsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}, "Items" -> {}, "ItemsIndexed" -> {}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\)]

Out[1]=

In[2]:=

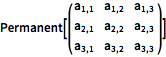
Permanent[\!\(\* TagBox[ RowBox[{"(", "", GridBox[{ { SubscriptBox["a", RowBox[{"1", ",", "1"}]], SubscriptBox["a", RowBox[{"1", ",", "2"}]], SubscriptBox["a", RowBox[{"1", ",", "3"}]]}, { SubscriptBox["a", RowBox[{"2", ",", "1"}]], SubscriptBox["a", RowBox[{"2", ",", "2"}]], SubscriptBox["a", RowBox[{"2", ",", "3"}]]}, { SubscriptBox["a", RowBox[{"3", ",", "1"}]], SubscriptBox["a", RowBox[{"3", ",", "2"}]], SubscriptBox["a", RowBox[{"3", ",", "3"}]]} }, GridBoxAlignment->{ "Columns" -> {{Left}}, "ColumnsIndexed" -> {}, "Rows" -> {{Baseline}}, "RowsIndexed" -> {}, "Items" -> {}, "ItemsIndexed" -> {}}, GridBoxSpacings->{"Columns" -> { Offset[0.27999999999999997`], { Offset[0.7]}, Offset[0.27999999999999997`]}, "ColumnsIndexed" -> {}, "Rows" -> { Offset[0.2], { Offset[0.4]}, Offset[0.2]}, "RowsIndexed" -> {}, "Items" -> {}, "ItemsIndexed" -> {}}], "", ")"}], Function[BoxForm`e$, MatrixForm[BoxForm`e$]]]\)]

Out[2]=

모든 요소가 1인 행렬에 Permanent를 적용하는 것은 재미있는 생각이지만, 계승 함수를 계산하는 비효율적인 방법입니다.

In[3]:=

Table[Permanent[ConstantArray[1, {n, n}]], {n, 10}]

Out[3]=

영구식은 다음의 더 재미있는 조합 문제 해결에 사용할 수 있습니다. n개의 집합이 주어지고, 각각의 부분 집합 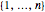을 포함하는 경우, 각 부분 집합에서 다른 요소를 선택하는 방법은 몇 가지나 있을지 생각해 봅니다. 먼저, 행렬 m을 구축합니다. 여기에서 부분 집합 i가 j를 포함할 때 (i, j)의 위치에 1을 포함하고 그렇지 않으면 0이 포함됩니다.

In[4]:=

sets = {{3, 5, 6, 7}, {3, 7}, {1, 2, 4, 5, 7}, {3}, {1, 3, 6}, {1, 5, 7}, {1, 2, 3, 6}}

Out[4]=

In[5]:=

m = Table[If[MemberQ[sets[[i]], j], 1, 0] , {i, 7}, {j, 7}]; m // MatrixForm

Out[5]//MatrixForm=

m의 영구식이 이 문제의 해법입니다.

In[6]:=

Permanent[m]

Out[6]=

모든 튜플을 명시적으로 구축하여 답을 확인합니다.

In[7]:=

Select[Tuples[sets], DuplicateFreeQ]

Out[7]=