Use the Smith Decomposition to Analyze a Lattice

Consider the lattice 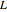generated by integer multiples of the vectors 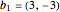and .

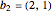In[1]:=

b1 = {3, -3}; b2 = {2, 1};

In[2]:=

ptsb = Flatten[Table[j b1 + k b2, {j, -12, 12}, {k, -12, 12}], 1];

In[3]:=

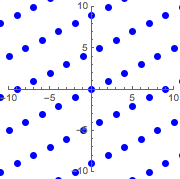
graphicsb = Graphics[{Blue, PointSize[Large], Point@ptsb}, PlotRange -> 10, Axes -> True]

Out[3]=

Let 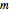be the matrix whose rows are 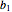and .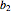

In[4]:=

m = {b1, b2};

The Smith decomposition gives three matrices that satisfy the identity .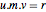

In[5]:=

{u, r, v} = SmithDecomposition[m];

In[6]:=

u.m.v == r

Out[6]=

The matrices 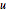and 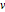have integer entries and determinant one.

In[7]:=

{u // MatrixForm, v // MatrixForm, Det[u], Det[v]}

Out[7]=

The matrix 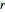is integer and diagonal. From its entries it can be seen that the structure of the group 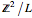is 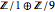or simply 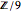, as 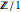is the trivial group.

In[8]:=

r // MatrixForm

Out[8]//MatrixForm=

Multiplying the identity 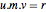on the right by 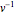gives 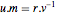. Because 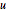is integer and determinant 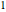, generates the same lattice as 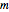but is simpler.

In[9]:=

g = r.Inverse[v]; g // MatrixForm

Out[9]//MatrixForm=

Visualize the lattice generated by the rows of .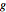

In[10]:=

ptsg = Flatten[ Table[j First[g] + k Last[g], {j, -12, 12}, {k, -12, 12}], 1];

In[11]:=

graphicsg = Graphics[{Red, PointSize[Medium], Point@ptsg}, PlotRange -> 10, Axes -> True]

Out[11]=

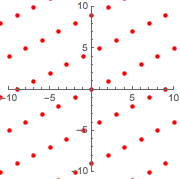
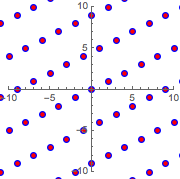
Superimposing the new lattice on the original confirms that they are the same.

In[12]:=

Show[{graphicsb, graphicsg}]

Out[12]=