非同次ポアソン過程
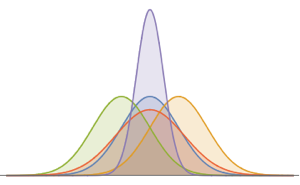
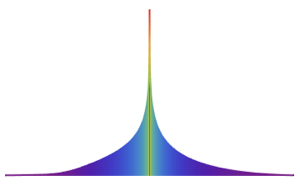
非同次ポアソン過程は，時間によって比が変動するポアソン過程である．これは，店を訪れる顧客の到着時間，トラフィックの事象，道路の損傷の位置をモデル化するのに使うことができる．任意時間スライス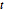 
における過程の確率密度関数はポアソン分布に従う．
In[1]:=
PDF[InhomogeneousPoissonProcess[f[\[Tau]], \[Tau]][t], x]Out[1]=
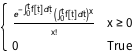
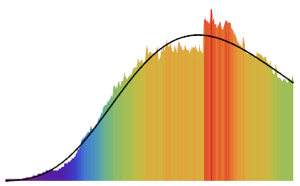
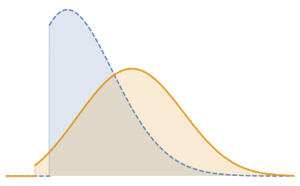
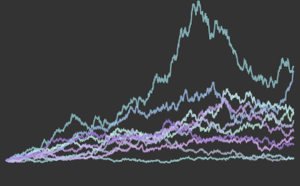
非同次ポアソン過程のシミュレーションを行う．
In[2]:=
td = RandomFunction[
InhomogeneousPoissonProcess[2 + 1/(1 + t^2), t], {0, 20}];完全なWolfram言語入力を表示する
Out[3]=
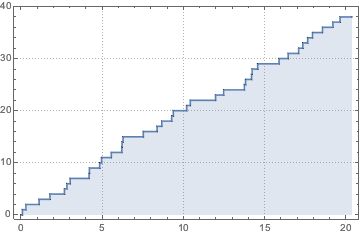
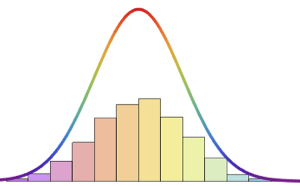
非同次ポアソン過程は，到着数をモデル化するのに使える．ここでは，小さなファーストフードレストランにおける客の到着数のシミュレーションを，顧客の1時間ごとの到着率が与えられた場合に行う．
In[4]:=
arrivalrates = {{0, 8}, {1, 9}, {2, 7}, {4, 6}, {5, 12}, {6, 14}, {7,
11}, {8, 6}, {9, 4}, {10, 3}, {11, 8}, {12, 15}, {13, 12}, {14,
10}, {15, 8}, {16, 6}, {17, 12}, {18, 17}, {19, 15}, {20,
12}, {21, 6}, {22, 5}, {23, 7}};
\[Lambda][t_] =
Interpolation[arrivalrates, InterpolationOrder -> 1][t];完全なWolfram言語入力を表示する
Out[5]=
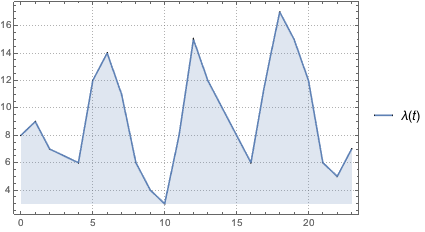
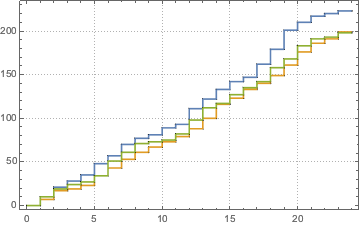
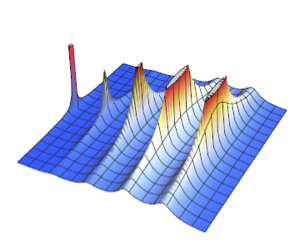
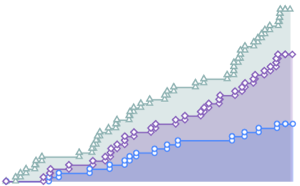
指定の比率関数 λ(t)に基づく到着について非同次ポアソン過程を定義し，1日の到着数のシミュレーションを行う．
In[6]:=
\[ScriptCapitalP] = InhomogeneousPoissonProcess[\[Lambda][t], t];
td = RandomFunction[\[ScriptCapitalP], {0, 23, 1}, 3];完全なWolfram言語入力を表示する
Out[7]=
