Wolfram Language™

Processo de Poisson não homogêneo

Um processo de Poisson não homogêneo é um processo com uma taxa de tempo variável. Ele pode ser usado para modelar os tempos de chegada dos clientes em uma loja, eventos de tráfego, e as posições dos danos ao longo de uma estrada. A função densidade de probabilidade do processo em qualquer fatia de tempo t é uma distribuição de Poisson.

In[1]:=

PDF[InhomogeneousPoissonProcess[f[\[Tau]], \[Tau]][t], x]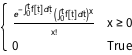

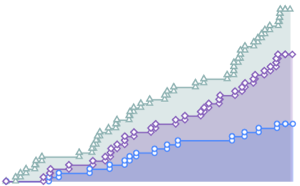
Out[1]=

Simule um processo de Poisson não homogêneo.

In[2]:=

td = RandomFunction[ InhomogeneousPoissonProcess[2 + 1/(1 + t^2), t], {0, 20}];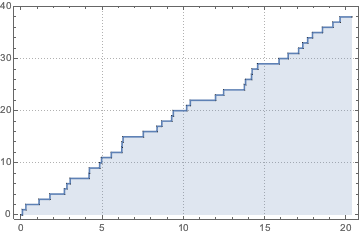

In[3]:=

ListStepPlot[td, Filling -> Axis, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[3]=

Um processo de Poisson não homogéneo pode ser utilizado para modelar as contagens de chegadas. Aqui, o processo é usado para simular o número de chegadas em um pequeno restaurante de fast-food se as taxas de chegada de clientes por horas são dadas.

In[4]:=

arrivalrates = {{0, 8}, {1, 9}, {2, 7}, {4, 6}, {5, 12}, {6, 14}, {7, 11}, {8, 6}, {9, 4}, {10, 3}, {11, 8}, {12, 15}, {13, 12}, {14, 10}, {15, 8}, {16, 6}, {17, 12}, {18, 17}, {19, 15}, {20, 12}, {21, 6}, {22, 5}, {23, 7}}; \[Lambda][t_] = Interpolation[arrivalrates, InterpolationOrder -> 1][t];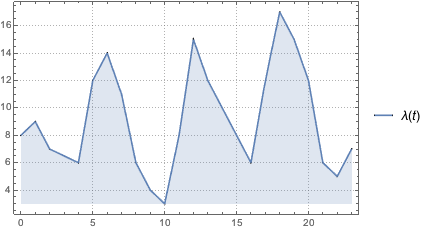

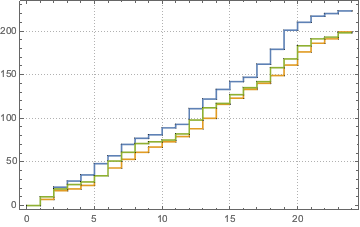
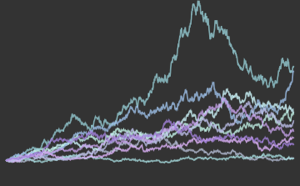
In[5]:=

Plot[\[Lambda][t], {t, 0, 23}, Exclusions -> None, Filling -> Axis, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[5]=

Defina um processo de Poisson não homogêneo para as chegadas com base na função de taxa de deternminada λ(t) e simule a contagem de chegadas em um dia.

In[6]:=

\[ScriptCapitalP] = InhomogeneousPoissonProcess[\[Lambda][t], t]; td = RandomFunction[\[ScriptCapitalP], {0, 23, 1}, 3];

In[7]:=

ListStepPlot[td, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[7]=