非齐次泊松过程: Wolfram 语言 11 的新功能

‹›

非齐次泊松过程

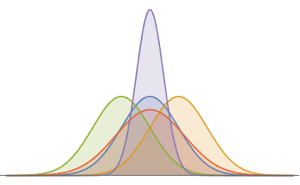
非齐次泊松过程是一个有时变变化率的泊松过程. 它可用于构建关于客户达到店铺时间、交通事故和道路损坏位置的模型. 过程在任何时间段 t 的概率密度函数是泊松分布.

In[1]:=

PDF[InhomogeneousPoissonProcess[f[\[Tau]], \[Tau]][t], x]

Out[1]=

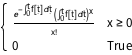
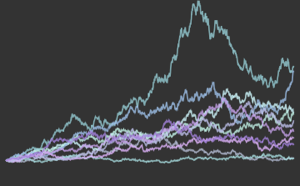
模拟一个非齐次泊松过程.

In[2]:=

td = RandomFunction[
   InhomogeneousPoissonProcess[2 + 1/(1 + t^2), t], {0, 20}];

显示完整的 Wolfram 语言输入

In[3]:=

ListStepPlot[td, Filling -> Axis, ImageSize -> Medium, 
 PlotTheme -> "Detailed"]

Out[3]=

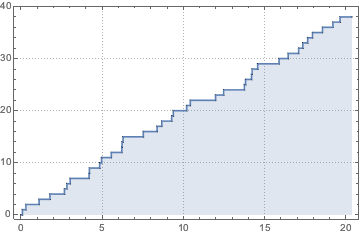
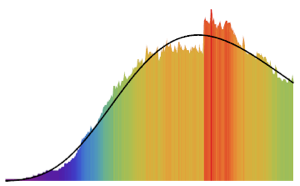
非齐次泊松过程可用于模拟到达计数模型. 这里，在客户每小时的到达频率给定情况下，用该过程对到达小快餐店的人数进行模拟.

In[4]:=

arrivalrates = {{0, 8}, {1, 9}, {2, 7}, {4, 6}, {5, 12}, {6, 14}, {7, 
    11}, {8, 6}, {9, 4}, {10, 3}, {11, 8}, {12, 15}, {13, 12}, {14, 
    10}, {15, 8}, {16, 6}, {17, 12}, {18, 17}, {19, 15}, {20, 
    12}, {21, 6}, {22, 5}, {23, 7}};
\[Lambda][t_] = 
  Interpolation[arrivalrates, InterpolationOrder -> 1][t];

显示完整的 Wolfram 语言输入

In[5]:=

Plot[\[Lambda][t], {t, 0, 23}, Exclusions -> None, Filling -> Axis, 
 ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[5]=

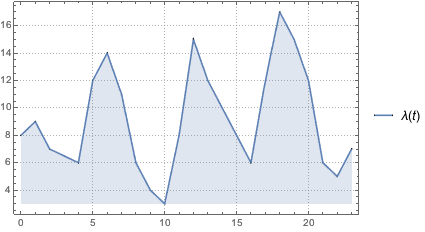
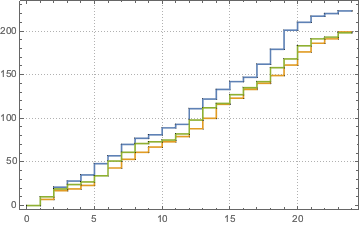
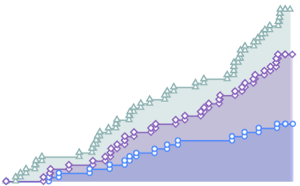
根据给定频率函数 λ(t)，定义一个到达人数的非齐次泊松过程并模拟一天中的到达人数.

In[6]:=

\[ScriptCapitalP] = InhomogeneousPoissonProcess[\[Lambda][t], t];
td = RandomFunction[\[ScriptCapitalP], {0, 23, 1}, 3];

显示完整的 Wolfram 语言输入

In[7]:=

ListStepPlot[td, ImageSize -> Medium, PlotTheme -> "Detailed"]

Out[7]=

Wolfram 语言™

非齐次泊松过程

相关范例