Wolfram言語™

株価の対数利益率

古典的なブラック・ショールズ(Black–Scholes)モデルにおいて幾何ブラウン(Brownian)運動でモデル化された株価は，その対数利益率において正規分布に従うと想定される．ここではその仮定をGoogle，Microsoft，Facebook，Apple，Intelの5社の株価を使って確かめる．

FinancialDataから2015年の株価を取り出す．

In[1]:=

symbols = {"GOOGL", "MSFT", "FB", "AAPL", "INTC"}; prices = Table[ FinancialData[stock, {{2015, 1, 1}, {2015, 12, 31}}], {stock, symbols}];

対数利益率を計算する．

In[2]:=

logreturn = Minus[Differences[Log[prices[[All, All, 2]]], {0, 1}]];

次数1のARCHProcessで対数利益率にフィルタを掛ける．

In[3]:=

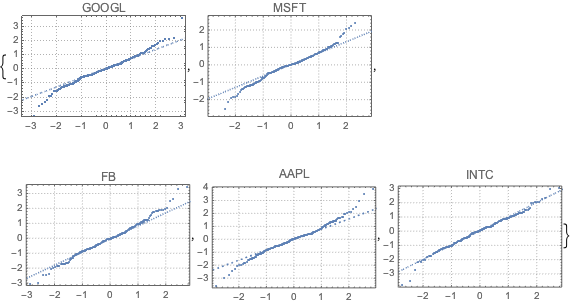
fdata = Table[ {\[Kappa]1, \[Alpha]1} = {\[Kappa], \[Alpha]} /. FindProcessParameters[lr, ARCHProcess[\[Kappa], {\[Alpha]}]]; MovingMap[Last[#]/Sqrt[\[Kappa]1 + \[Alpha]1 First[#]^2] &, lr, 2] , {lr, logreturn}]; fdata = Transpose[fdata];

各株からのフィルタを掛けたデータと正規分布をQuantilePlotを使って比べる．5社すべてについて，裾部は正規分布から逸脱する．

In[4]:=

MapThread[ QuantilePlot[#1, PlotLabel -> #2, PlotTheme -> "Detailed"] &, {Transpose[fdata], symbols}]

Out[4]=

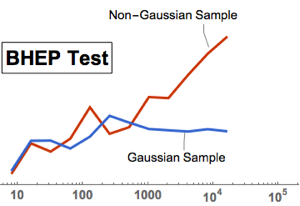
多変量の正規性検定をBaringhausHenzeTest (BHEP)を使って行う．正規性の仮定は明らかに棄却されている．

In[5]:=

htd = BaringhausHenzeTest[fdata, "HypothesisTestData"];

In[6]:=

htd["TestDataTable"]

Out[6]=

In[7]:=

htd["ShortTestConclusion"]

Out[7]=

フィルタを掛けたデータをMultinormalDistributionとMultivariateTDistributionを使ってフィットする．

In[8]:=

multiN = EstimatedDistribution[fdata, MultinormalDistribution[Array[x, 5], Array[s, {5, 5}]]]

Out[8]=

In[9]:=

multiT = EstimatedDistribution[fdata, MultivariateTDistribution[Array[x, 5], Array[s, {5, 5}], nu]]

Out[9]=

2つの分布について赤池情報量基準（AIC）を計算する．MultivariateTDistributionのモデルの方が小さな値を持つ．

In[10]:=

aic[k_, dist_, data_] := 2 k - 2 LogLikelihood[dist, data]

In[11]:=

aic[5 + 15, multiN, fdata]

Out[11]=

In[12]:=

aic[5 + 15 + 1, multiT, fdata]

Out[12]=