股票价格的对数收益

几何布朗运动建模（古典布莱克-舒尔斯模型) 的股票价格，其对数收益被假设为正态分布. 在此，用 Google、Microsoft、Facebook、Apple 和 Intel 这 5 家公司的股票价格对该假设进行了检验.

用 FinancialData 提取 2015 年的股票价格.

In[1]:=

symbols = {"GOOGL", "MSFT", "FB", "AAPL", "INTC"}; prices = Table[ FinancialData[stock, {{2015, 1, 1}, {2015, 12, 31}}], {stock, symbols}];

计算对数收益.

In[2]:=

logreturn = Minus[Differences[Log[prices[[All, All, 2]]], {0, 1}]];

用 1 阶 ARCHProcess 过滤对数收益.

In[3]:=

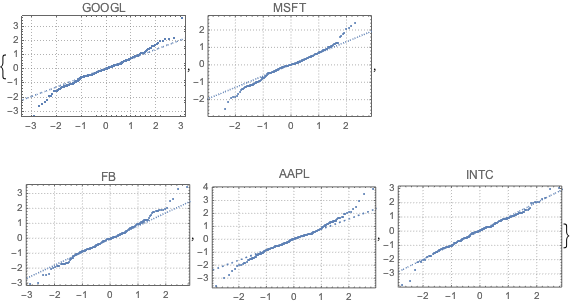
fdata = Table[ {\[Kappa]1, \[Alpha]1} = {\[Kappa], \[Alpha]} /. FindProcessParameters[lr, ARCHProcess[\[Kappa], {\[Alpha]}]]; MovingMap[Last[#]/Sqrt[\[Kappa]1 + \[Alpha]1 First[#]^2] &, lr, 2] , {lr, logreturn}]; fdata = Transpose[fdata];

通过 QuantilePlot 将每个股票的过滤数据与正态分布进行对比. 全部 5 家公司的尾部都从正态偏离.

In[4]:=

MapThread[ QuantilePlot[#1, PlotLabel -> #2, PlotTheme -> "Detailed"] &, {Transpose[fdata], symbols}]

Out[4]=

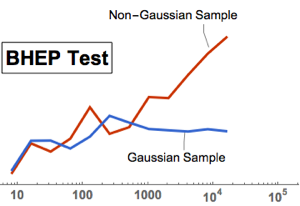
用 BaringhausHenzeTest（BHEP）进行多元正态性检验. 正态性假设被明确驳回.

In[5]:=

htd = BaringhausHenzeTest[fdata, "HypothesisTestData"];

In[6]:=

htd["TestDataTable"]

Out[6]=

In[7]:=

htd["ShortTestConclusion"]

Out[7]=

用 MultinormalDistribution 和 MultivariateTDistribution 拟合过滤数据.

In[8]:=

multiN = EstimatedDistribution[fdata, MultinormalDistribution[Array[x, 5], Array[s, {5, 5}]]]

Out[8]=

In[9]:=

multiT = EstimatedDistribution[fdata, MultivariateTDistribution[Array[x, 5], Array[s, {5, 5}], nu]]

Out[9]=

计算两个分布的 AIC. MultivariateTDistribution 模型的值要小一些.

In[10]:=

aic[k_, dist_, data_] := 2 k - 2 LogLikelihood[dist, data]

In[11]:=

aic[5 + 15, multiN, fdata]

Out[11]=

In[12]:=

aic[5 + 15 + 1, multiT, fdata]

Out[12]=