重さを量る
重力場にあるオブジェクトの重さは,その質量とそのオブジェクトがある位置での重力場の値の積である.地表では重力場は一定ではないため,オブジェクトの重さは場所によって異なる.この例では,標高と緯度により重力場の大きさがどのように変化するかを調べてみる.
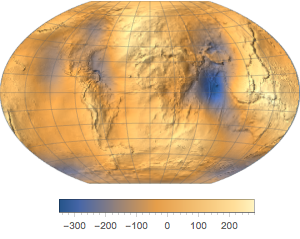
GeogravityModelDataは指定された地点における地球の重力場の特性をいくつか計算する.
In[1]:=
GeogravityModelData[GeoPosition[{0, 0}]]Out[1]=

これはGeoElevationDataによって提供される地理的標高を使う.
In[2]:=
GeoElevationData[GeoPosition[{0, 0}]]Out[2]=
他の要素の影響を無視すると,緯度が同じくらいであれば,標高がより高い地点の重力場の方が通常小さい.
In[3]:=
GeoPosition[Entity["City", {"Quito", "Pichincha", "Ecuador"}]]Out[3]=
In[4]:=
GeoPosition[Entity["City", {"Quito", "Pichincha", "Ecuador"}]];
{GeoElevationData[%, UnitSystem -> "Metric"],
GeogravityModelData[%, "Magnitude"]}Out[4]=
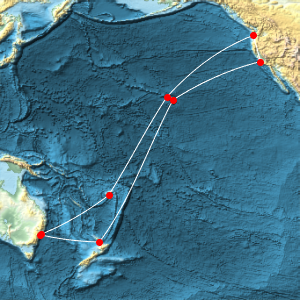
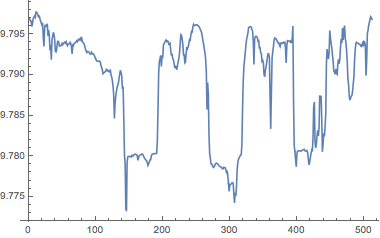
赤道上の等距離の地点における重力場の値を計算する.
In[5]:=

equatorialgravity =
GeogravityModelData[{GeoPosition[{0, -180}], GeoPosition[{5, 180}]},
"Magnitude"][[1]]Out[5]=

In[6]:=
ListPlot[equatorialgravity, Joined -> True]Out[6]=
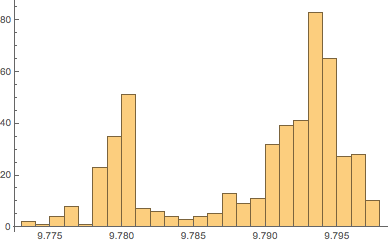
下のヒストグラムには,陸地の部分と海底に対応して,大きいピークが2つある.
In[7]:=
Histogram[equatorialgravity, 20]Out[7]=
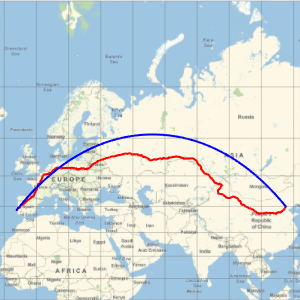
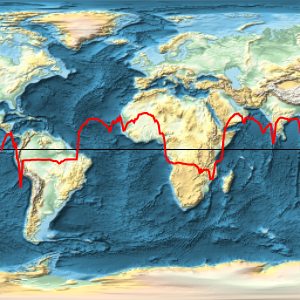
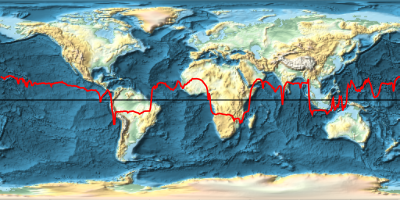
地球の起伏図に重力場の大きさを重ねる.
In[8]:=

equatorialgravityplot =
ListPlot[equatorialgravity, Axes -> False, Joined -> True,
AspectRatio -> 1/8, PlotRangePadding -> None, ImagePadding -> None,
ImageSize -> 400, PlotStyle -> Red];In[9]:=
worldmap =
GeoGraphics[GeoPath["Equator"], GeoRange -> "World",
ImageSize -> 400, GeoBackground -> "ReliefMap"];In[10]:=
Overlay[{worldmap, equatorialgravityplot}, Alignment -> Center]Out[10]=
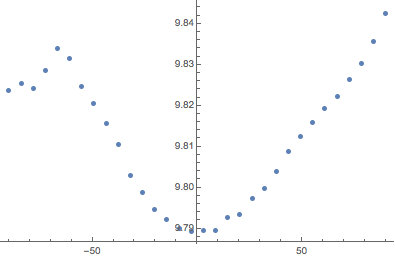
緯度についての変化を示すために,経度上の重力場の大きさを平均し,緯度に対する結果を表す.
In[11]:=

gravity =
Mean /@ GeogravityModelData[{GeoPosition[{-90, -180}],
GeoPosition[{90, 180}]}, "Magnitude"];低緯度では南極は高度が高いため明らかに重力場の影響が見られる.
In[12]:=
ListPlot[gravity, DataRange -> {-90, 90}]Out[12]=
In[13]:=
MinMax[gravity]Out[13]=
したがって,指定されたオブジェクトをどこで量るかによって,その重さが0.5%ほど異なる可能性がある.
In[14]:=
MinMax[gravity];
1 - First[%]/Last[%]