重量是多少?
一个物体在重力场中的重量是其质量和在该物体所处重力场的乘积. 地球表面的重力场不是恒定的,因此相同物体的重量在不同位置有所变化. 本例对重力场的大小随海拔和纬度的变化进行了考察.
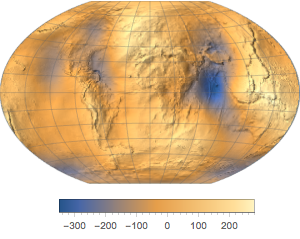
GeogravityModelData 计算地球重力场在给定位置上的几个属性.
In[1]:=
GeogravityModelData[GeoPosition[{0, 0}]]Out[1]=

其使用了 GeoElevationData 提供的地形海拔.
In[2]:=
GeoElevationData[GeoPosition[{0, 0}]]Out[2]=
忽略其他影响,在纬度相近而海拔更高的位置上,重力场一般较小.
In[3]:=
GeoPosition[Entity["City", {"Quito", "Pichincha", "Ecuador"}]]Out[3]=
In[4]:=
GeoPosition[Entity["City", {"Quito", "Pichincha", "Ecuador"}]];
{GeoElevationData[%, UnitSystem -> "Metric"],
GeogravityModelData[%, "Magnitude"]}Out[4]=
计算在赤道等分点重力场的大小.
In[5]:=

equatorialgravity =
GeogravityModelData[{GeoPosition[{0, -180}], GeoPosition[{5, 180}]},
"Magnitude"][[1]]Out[5]=

In[6]:=
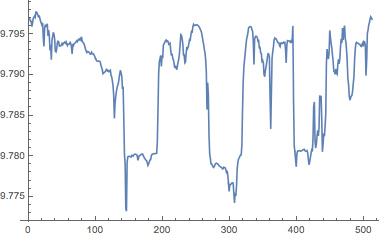
ListPlot[equatorialgravity, Joined -> True]Out[6]=
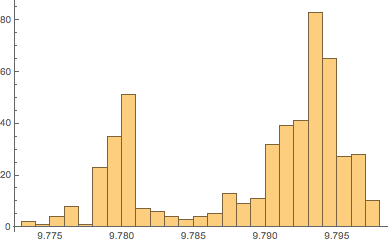
下面的直方图有两个峰值,分别对应陆地区域和海洋底部.
In[7]:=
Histogram[equatorialgravity, 20]Out[7]=
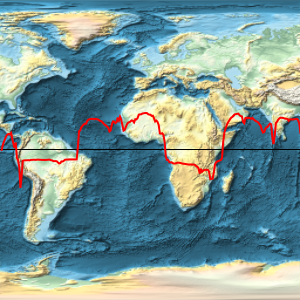
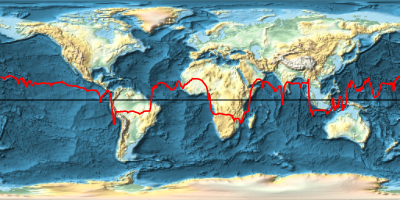
将重力场大小覆盖在地球的地势图上.
In[8]:=

equatorialgravityplot =
ListPlot[equatorialgravity, Axes -> False, Joined -> True,
AspectRatio -> 1/8, PlotRangePadding -> None, ImagePadding -> None,
ImageSize -> 400, PlotStyle -> Red];In[9]:=
worldmap =
GeoGraphics[GeoPath["Equator"], GeoRange -> "World",
ImageSize -> 400, GeoBackground -> "ReliefMap"];In[10]:=
Overlay[{worldmap, equatorialgravityplot}, Alignment -> Center]Out[10]=
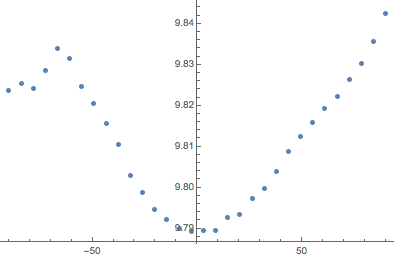
为显示随纬度的变化,我们在经度上对重力场大小进行平均,并相对纬度显示其结果.
In[11]:=

gravity =
Mean /@ GeogravityModelData[{GeoPosition[{-90, -180}],
GeoPosition[{90, 180}]}, "Magnitude"];由于添加了海拔,南极洲有一个明显的低纬度效应.
In[12]:=
ListPlot[gravity, DataRange -> {-90, 90}]Out[12]=
In[13]:=
MinMax[gravity]Out[13]=
因此,根据测量地点的不同,一个给定物体的重量可能会有 0.5% 的变化.
In[14]:=
MinMax[gravity];
1 - First[%]/Last[%]