Spherical or Ellipsoidal Mercator

The Mercator projection produces different results with a spherical model of the Earth and an ellipsoidal model of the Earth. The Wolfram Language allows you to work with both situations.

The projection used in most map web servers uses a spherical model of the Earth, and it is usually called "web Mercator".

In[1]:=

webMercator = {"Mercator", "ReferenceModel" -> GeodesyData["WGS84", "SemimajorAxis"]}

Out[1]=

In[2]:=

ellipMercator = {"Mercator", "ReferenceModel" -> "WGS84"}

Out[2]=

Transform the location of the University of Oxford using both projections.

In[3]:=

p = GeoPosition[ Entity["University", "UniversityOfOxfordUnitedKingdom36022"]]

Out[3]=

In[4]:=

GeoGridPosition[p, webMercator][[1]]

Out[4]=

In[5]:=

GeoGridPosition[p, ellipMercator][[1]]

Out[5]=

There is a difference corresponding to more than 33 kilometers in the northing coordinate.

In[6]:=

GeoGridPosition[p, webMercator][[1]]; GeoGridPosition[p, ellipMercator][[1]]; %% - %

Out[6]=

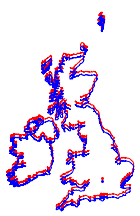
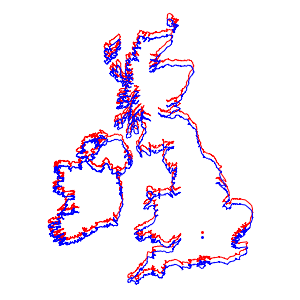
Using both projections, draw respective maps of the UK and Ireland, which look nearly identical.

In[7]:=

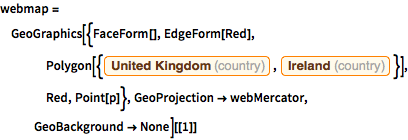
webmap = GeoGraphics[{FaceForm[], EdgeForm[Red], Polygon[{Entity["Country", "UnitedKingdom"], Entity["Country", "Ireland"]}], Red, Point[p]}, GeoProjection -> webMercator, GeoBackground -> None][[1]]

Out[7]=

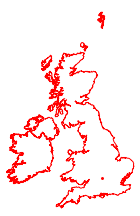
In[8]:=

ellipmap = GeoGraphics[{FaceForm[], EdgeForm[Blue], Polygon[{Entity["Country", "UnitedKingdom"], Entity["Country", "Ireland"]}], Blue, Point[p]}, GeoProjection -> ellipMercator, GeoBackground -> None][[1]]

Out[8]=

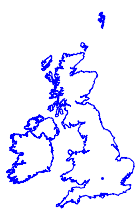
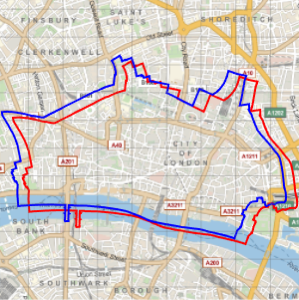
However, when overlaid on the same map, you can clearly see the difference.

In[9]:=

Show[webmap, ellipmap]

Out[9]=