UPS and UTM Projections
The UTM (Universal Transverse Mercator) family of projections is widely used in applications. In Version 11, there are now both North and South UTM zone projections, avoiding the use of negative northings, as is usual in practice. The UTM projections cannot reach the poles, and they are usually supplemented with two UPS (Universal Polar Stereographic) charts, now also supported.
This list now contains the 60 UTM North zones and the respective 60 UTM South zones.
Short[GeoProjectionData["UTMZone"], 3]
They are similarly defined, but have a different grid origin.
GeoProjectionData["UTMZone34"]GeoProjectionData["UTMZone34South"]These are the two UPS zones.
GeoProjectionData["UPSZone"]They are defined in terms of the Universal Polar Stereographic projection.
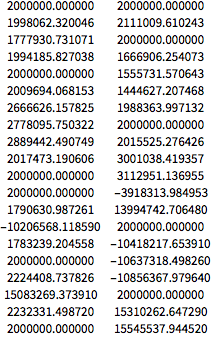
GeoProjectionData["UPSNorth"]GeoProjectionData["UPSSouth"]The Standardization Document NGA.SIG.0012_ 2.0.0_UTMUPS of the National Geospatial-Intelligence Agency provides various examples to check the accuracy of the algorithms. For example, for the UPS projection it gives the following examples in section 10.2.
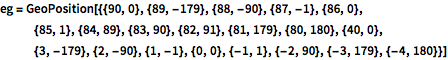
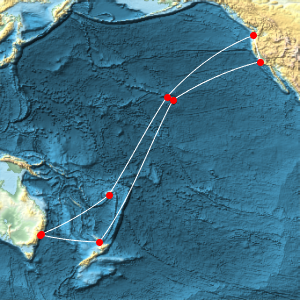
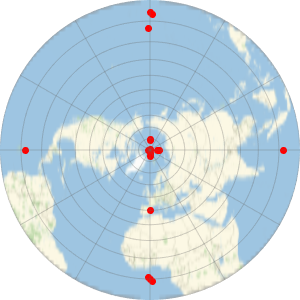
eg = GeoPosition[{{90, 0}, {89, -179}, {88, -90}, {87, -1}, {86,
0}, {85, 1}, {84, 89}, {83, 90}, {82, 91}, {81, 179}, {80,
180}, {40, 0}, {3, -179}, {2, -90}, {1, -1}, {0, 0}, {-1, 1}, {-2,
90}, {-3, 179}, {-4, 180}}]
Represent those points using a "UPSNorth" projection. Note that the North Pole is not at {0, 0} in the projected coordinates due to the nontrivial grid origin parameters.

GeoGraphics[{Red, PointSize[Large], Point[eg]},
GeoProjection -> {"UPSNorth", "Centering" -> {90, 0}},
GeoGridLines -> Automatic, GeoZoomLevel -> 3, Frame -> True]
These are the numbers obtained with the Wolfram Language, which coincide with those given in the Standardization Document to micrometer precision.
NumberForm[Grid[First@GeoGridPosition[eg, "UPSNorth"]], {13, 6},
ExponentFunction -> (Null &)]