Поиск связанных компонентов графика
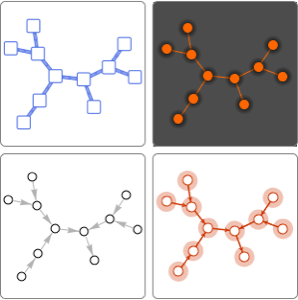
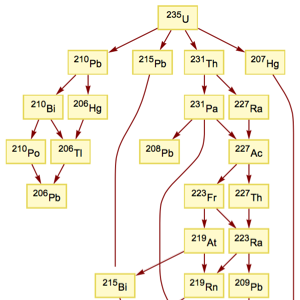
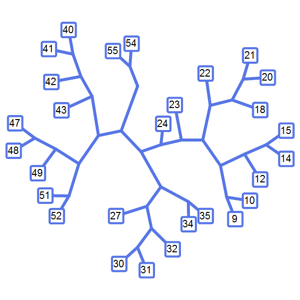
Смоделируйте сеть прыжков лягушки по листьям кувшинки. Версия 11 представляет функции ConnectedGraphComponents и WeaklyConnectedGraphComponents для анализа сетевого соединения.
Лягушка способна совершить прыжок длинной в 1,5 фута, чтобы перескочить с одной из 25 кувшинок на другую.
In[1]:=

lilyDensity =
MixtureDistribution[{1, 1,
1}, {BinormalDistribution[{0, 0}, {1, 1}, 0],
BinormalDistribution[{-1, 4}, {1, 1}, -1/2],
BinormalDistribution[{4, 4}, {1, 1}, 1/3]}];
lilyPond = SpatialGraphDistribution[25, 1.5, lilyDensity];Выберем пруд.
In[2]:=

g = RandomGraph[lilyPond, VertexShape -> \!\(\*
GraphicsBox[
{EdgeForm[{Hue[0.3277777777777778, 0.16216216216216217`, 1.], Opacity[
1.], AbsoluteThickness[1], CapForm["Round"]}], FaceForm[Hue[
0.2388888888888889, 1., 0.9224857536122444]],
PolygonBox[CompressedData["
1:eJxTTMoPSmViYGCQAmIQDQYVhQ5gWiALQkeUQmiDPAj9ohxCcxRB6IwKCF1R
DKF3QOVnlKDqvwGlT0DNzyiD0AE5ENoCyr+QBOVD9StEoupz8IHqy4XQDeZQ
fiqEZtCG0AvioXxdVHMabKD8YKh5flDaG0I/iIbynaDuSYbqs4bQH2D2WkLo
Dqg7HXwh9A+o/xdEQOgZVVD3Qc2xqIbQE9Kh/oLKf4CFNzQ8N0DDBRZ+BTkO
ABBsOr4=
"]]},
ImageSize->{45., Automatic}]\), VertexSize -> {"Scaled", 0.1},
EdgeStyle -> Opacity[0], Background -> Hue[0.6, 0.8, 0.4],
ImageSize -> 150]Out[2]=
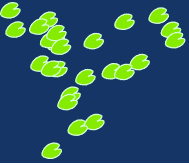
Найдем самое большое собрание кувшинок, по которым может прыгать лягушка.
In[3]:=
VertexCount[First[ConnectedGraphComponents[g]]]Out[3]=
Определим, сколько раз лягушка должна будет проплыть, чтобы попасть на все кувшинки.
In[4]:=
Length[ConnectedGraphComponents[g]] - 1Out[4]=