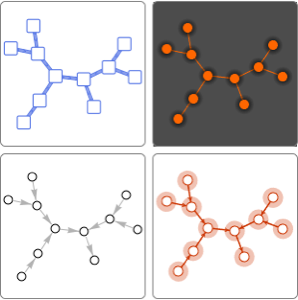
Zusammenhängende Graphenkomponenten finden
Modellieren Sie das Netz aus Sprüngen eines Frosches auf Basis der Seerosenblattdichte. Version 11 bietet nun die Funktionen ConnectedGraphComponents und WeaklyConnectedGraphComponents zur Analyse der Netzwerkkonnektivität.
Ein Frosch in einem Seerosenteich ist in der Lage, 45 cm weit zu springen, um sich von einem Seerosenblatt zum anderen fortzubewegen.
In[1]:=

lilyDensity =
MixtureDistribution[{1, 1,
1}, {BinormalDistribution[{0, 0}, {1, 1}, 0],
BinormalDistribution[{-1, 4}, {1, 1}, -1/2],
BinormalDistribution[{4, 4}, {1, 1}, 1/3]}];
lilyPond = SpatialGraphDistribution[25, 1.5, lilyDensity];Erstellen Sie einen Teich mit beliebigen Parametern.
In[2]:=

g = RandomGraph[lilyPond, VertexShape -> \!\(\*
GraphicsBox[
{EdgeForm[{Hue[0.3277777777777778, 0.16216216216216217`, 1.], Opacity[
1.], AbsoluteThickness[1], CapForm["Round"]}], FaceForm[Hue[
0.2388888888888889, 1., 0.9224857536122444]],
PolygonBox[CompressedData["
1:eJxTTMoPSmViYGCQAmIQDQYVhQ5gWiALQkeUQmiDPAj9ohxCcxRB6IwKCF1R
DKF3QOVnlKDqvwGlT0DNzyiD0AE5ENoCyr+QBOVD9StEoupz8IHqy4XQDeZQ
fiqEZtCG0AvioXxdVHMabKD8YKh5flDaG0I/iIbynaDuSYbqs4bQH2D2WkLo
Dqg7HXwh9A+o/xdEQOgZVVD3Qc2xqIbQE9Kh/oLKf4CFNzQ8N0DDBRZ+BTkO
ABBsOr4=
"]]},
ImageSize->{45., Automatic}]\), VertexSize -> {"Scaled", 0.1},
EdgeStyle -> Opacity[0], Background -> Hue[0.6, 0.8, 0.4],
ImageSize -> 150]Out[2]=

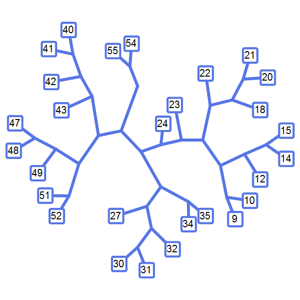
Ermitteln Sie die größte Menge Seerosenblätter, zwischen denen der Frosch hin- und herspringen kann.
In[3]:=
VertexCount[First[ConnectedGraphComponents[g]]]Out[3]=
Ermitteln Sie, wie oft der Frosch schwimmen müsste, um alle Seerosenblätter zu besuchen.
In[4]:=
Length[ConnectedGraphComponents[g]] - 1Out[4]=