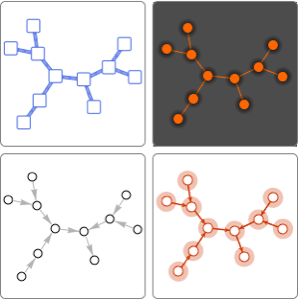
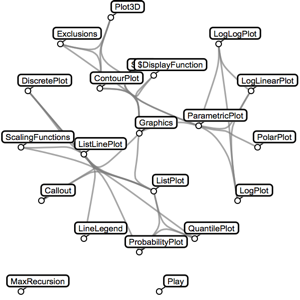
找出图的连通分量: Wolfram语言 11 的新功能

找出图的连通分量

根据荷叶密度模拟青蛙跳网络. 版本11 引入了 ConnectedGraphComponents 和 WeaklyConnectedGraphComponents 函数用于网络连通性分析.

荷花池中的青蛙要从 25 片荷叶中的一片跳到另一片上面，它一跳能够跳 1.5 英尺.

In[1]:=

lilyDensity = 
  MixtureDistribution[{1, 1, 
    1}, {BinormalDistribution[{0, 0}, {1, 1}, 0], 
    BinormalDistribution[{-1, 4}, {1, 1}, -1/2], 
    BinormalDistribution[{4, 4}, {1, 1}, 1/3]}];
lilyPond = SpatialGraphDistribution[25, 1.5, lilyDensity];

随机取样一个荷花池.

In[2]:=

g = RandomGraph[lilyPond, VertexShape -> \!\(\*
GraphicsBox[
{EdgeForm[{Hue[0.3277777777777778, 0.16216216216216217`, 1.], Opacity[
       1.], AbsoluteThickness[1], CapForm["Round"]}], FaceForm[Hue[
       0.2388888888888889, 1., 0.9224857536122444]], 
       PolygonBox[CompressedData["
1:eJxTTMoPSmViYGCQAmIQDQYVhQ5gWiALQkeUQmiDPAj9ohxCcxRB6IwKCF1R
DKF3QOVnlKDqvwGlT0DNzyiD0AE5ENoCyr+QBOVD9StEoupz8IHqy4XQDeZQ
fiqEZtCG0AvioXxdVHMabKD8YKh5flDaG0I/iIbynaDuSYbqs4bQH2D2WkLo
Dqg7HXwh9A+o/xdEQOgZVVD3Qc2xqIbQE9Kh/oLKf4CFNzQ8N0DDBRZ+BTkO
ABBsOr4=
"]]},
ImageSize->{45., Automatic}]\), VertexSize -> {"Scaled", 0.1}, 
  EdgeStyle -> Opacity[0], Background -> Hue[0.6, 0.8, 0.4], 
  ImageSize -> 150]

Out[2]=

找出青蛙可以在之间跳跃的最大的荷叶集.

In[3]:=

VertexCount[First[ConnectedGraphComponents[g]]]

Out[3]=

找出青蛙要访问所有的荷叶而需要游水的次数.

In[4]:=

Length[ConnectedGraphComponents[g]] - 1

Out[4]=

Wolfram 语言™

找出图的连通分量

相关范例