Wolfram Language™

Modele la composición del universo en el tiempo

Explore cómo la composición del universo cambia con el tiempo, de acuerdo con el modelo estándar ΛCDM (Lambda de materia oscura fría).

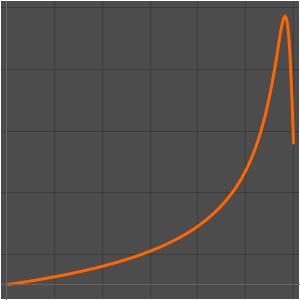
Calcule los valores de los índices de densidad de energía, materia y radiación oscura en distintas edades del universo, que van desde los 1000 a l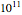os años.

In[1]:=

ages = Quantity[10^Range[3, 11, 0.2], "Years"];

In[2]:=

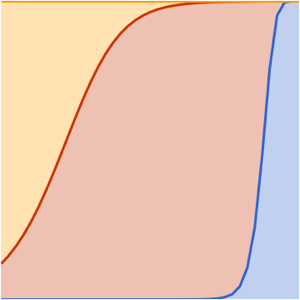
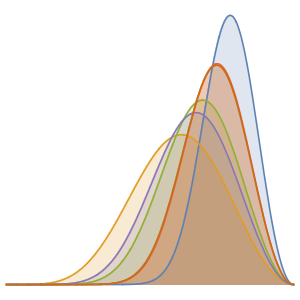
darkenergy = Table[UniverseModelData[t, "DarkEnergyDensityRatio"], {t, ages}]; matter = Table[ UniverseModelData[t, "MatterEnergyDensityRatio"], {t, ages}]; radiation = Table[UniverseModelData[t, "RadiationEnergyDensityRatio"], {t, ages}];

Represente la evolución en el tiempo de tres componentes, denotando la edad actual del universo con una barra vertical. Actualmente el componente más grande es la energía oscura.

In[3]:=

data = { Transpose[{ages, darkenergy}], Transpose[{ages, darkenergy + matter}], Transpose[{ages, darkenergy + matter + radiation}] }; ListLogLinearPlot[data, PlotRange -> All, Joined -> True, Filling -> {1 -> Axis, 2 -> {1}, 3 -> {2}}, FrameLabel -> Automatic, GridLines -> {{13.8*10^9}, None}, PlotRangePadding -> 0, Frame -> True, PlotLegends -> {"DarkEnergyDensity", "MatterEnergyDensity", "RadiationEnergyDensity"}]

Out[3]=

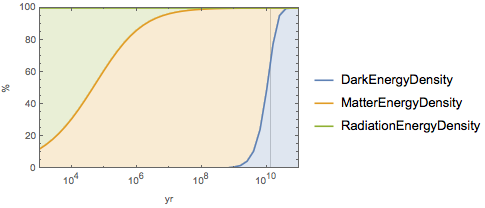
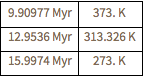
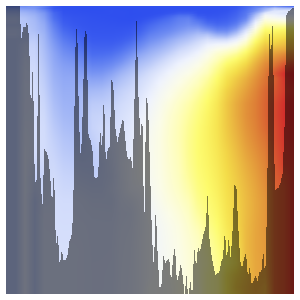
Descubra cuando la temperatura de la radiación de fondo hubiera estado entre los 273 y 373 K (la "Época habitable" del universo).

In[4]:=

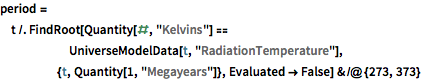
period = t /. FindRoot[ Quantity[#, "Kelvins"] == UniverseModelData[t, "RadiationTemperature"], {t, Quantity[1, "Megayears"]}, Evaluated -> False] & /@ {273, 373}

Out[4]=

In[5]:=

Grid[{#, UniverseModelData[#, "RadiationTemperature"]} & /@ Through[{Min, Mean, Max}[period]], Dividers -> All]

Out[5]=