Wolfram Language™

Modele a composição do universo ao longo do tempo

Explore como a composição do universo muda ao longo do tempo, de acordo com o modelo padrão ΛCDM (Lambda-matéria escura fria).

Calcule os valores dos índices de densidade da energia, matéria e radiação escura em diferentes idades do universo, que vão de 1000 a 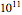anos.

In[1]:=

ages = Quantity[10^Range[3, 11, 0.2], "Years"];

In[2]:=

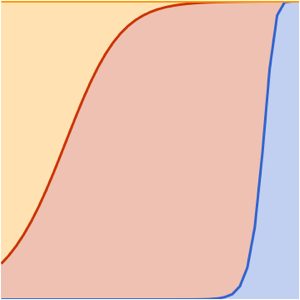
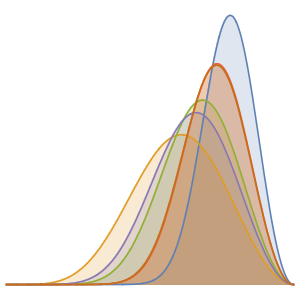
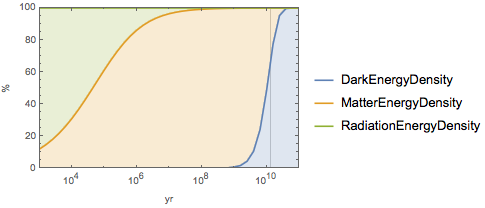
darkenergy = Table[UniverseModelData[t, "DarkEnergyDensityRatio"], {t, ages}]; matter = Table[ UniverseModelData[t, "MatterEnergyDensityRatio"], {t, ages}]; radiation = Table[UniverseModelData[t, "RadiationEnergyDensityRatio"], {t, ages}];

Represente a evolução no tempo para os três componentes, denotando a idade atual do universo com uma barra vertical. Atualmente o maior componente é a energia escura.

In[3]:=

data = { Transpose[{ages, darkenergy}], Transpose[{ages, darkenergy + matter}], Transpose[{ages, darkenergy + matter + radiation}] }; ListLogLinearPlot[data, PlotRange -> All, Joined -> True, Filling -> {1 -> Axis, 2 -> {1}, 3 -> {2}}, FrameLabel -> Automatic, GridLines -> {{13.8*10^9}, None}, PlotRangePadding -> 0, Frame -> True, PlotLegends -> {"DarkEnergyDensity", "MatterEnergyDensity", "RadiationEnergyDensity"}]

Out[3]=

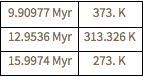
Descubra quando a temperatura da radiação de fundo teria sido entre 273 e 373 K (a "época habitável" do universo).

In[4]:=

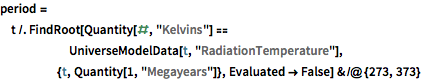
period = t /. FindRoot[ Quantity[#, "Kelvins"] == UniverseModelData[t, "RadiationTemperature"], {t, Quantity[1, "Megayears"]}, Evaluated -> False] & /@ {273, 373}

Out[4]=

In[5]:=

Grid[{#, UniverseModelData[#, "RadiationTemperature"]} & /@ Through[{Min, Mean, Max}[period]], Dividers -> All]

Out[5]=