長期間に渡る宇宙の構成をモデル化する

標準Λ-CDM（Λのコールドダークマター）モデルに基づいて，長期間に渡って宇宙の構成がどのように変化するかを調べる．

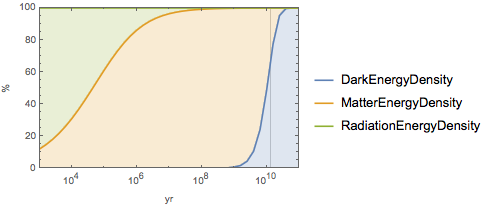
1000年から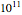年にかけての宇宙のさまざまな年齢における暗黒エネルギー，物質，放射線の密度率の値を計算する．

In[1]:=

ages = Quantity[10^Range[3, 11, 0.2], "Years"];

In[2]:=

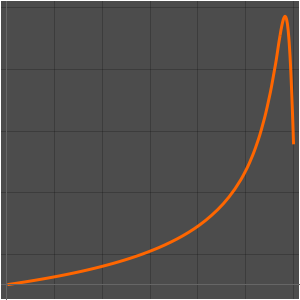
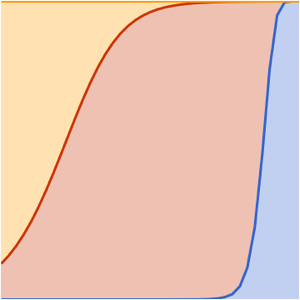
darkenergy = Table[UniverseModelData[t, "DarkEnergyDensityRatio"], {t, ages}]; matter = Table[ UniverseModelData[t, "MatterEnergyDensityRatio"], {t, ages}]; radiation = Table[UniverseModelData[t, "RadiationEnergyDensityRatio"], {t, ages}];

宇宙の現在の年齢を垂直線で示し，3つの構成要素について時間の経過に伴う進化を表す．現在最も大きな構成要素は暗黒エネルギーである．

In[3]:=

data = { Transpose[{ages, darkenergy}], Transpose[{ages, darkenergy + matter}], Transpose[{ages, darkenergy + matter + radiation}] }; ListLogLinearPlot[data, PlotRange -> All, Joined -> True, Filling -> {1 -> Axis, 2 -> {1}, 3 -> {2}}, FrameLabel -> Automatic, GridLines -> {{13.8*10^9}, None}, PlotRangePadding -> 0, Frame -> True, PlotLegends -> {"DarkEnergyDensity", "MatterEnergyDensity", "RadiationEnergyDensity"}]

Out[3]=

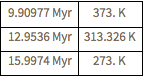
背景放射の温度が273ケルビンから373ケルビンの間であった時期（宇宙の「居住可能な元紀」 ）を求める．

In[4]:=

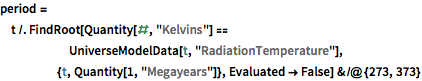
period = t /. FindRoot[ Quantity[#, "Kelvins"] == UniverseModelData[t, "RadiationTemperature"], {t, Quantity[1, "Megayears"]}, Evaluated -> False] & /@ {273, 373}

Out[4]=

In[5]:=

Grid[{#, UniverseModelData[#, "RadiationTemperature"]} & /@ Through[{Min, Mean, Max}[period]], Dividers -> All]

Out[5]=