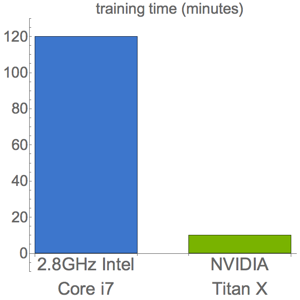
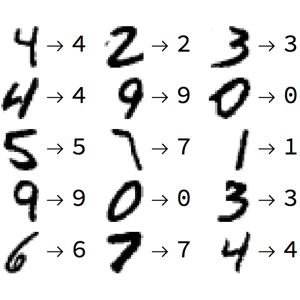Aprenda uma parametrização de uma variedade
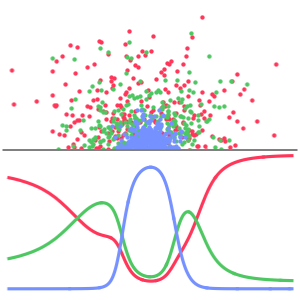
Aprenda uma parametrização de uma variedade junto com os dados de entrada correspondentes usando autoencoder, uma rede com uma layer de "gargalo"que aprende a reconstruir a entrada original.
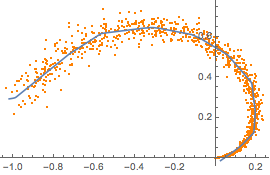
Amostras de dados de treinamento de uma parte de uma variedade sintéticos de duas dimensões.

manifold =
Table[AngleVector[{x, 0.9 Pi x}] +
x/20*RandomVariate[NormalDistribution[], 2], {x, 0, 1, 0.001}];
plot = ListPlot[manifold, PlotStyle -> Orange]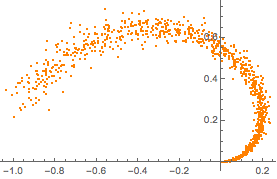
Crie uma rede com uma camada de "gargalo" para aprender uma parametrização da variedade.
net = NetChain[{25, Ramp, 1, 25, Ramp, 2}, "Input" -> 2]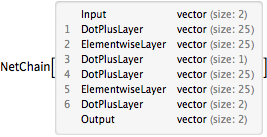
Crie uma rede de perda que calcula uma perda baseada no "erro de reconstrução"—uma medida do grau em que a rede pode produzir uma saída que é idêntica à sua entrada.
lossNet =
NetGraph[{net, MeanSquaredLossLayer[]}, {1 -> 2,
NetPort["Input"] -> NetPort[2, "Target"]}]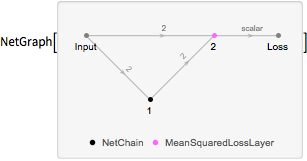
Treine a rede de perda na variedade e extraia a rede original da rede de perda.
lossNet =
NetTrain[lossNet, <|"Input" -> manifold|>, BatchSize -> 4096];
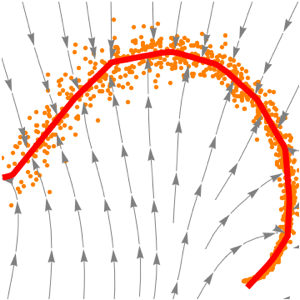
trained = NetExtract[lossNet, 1];Visualize como a rede projeta pontos arbitrários na variedade.
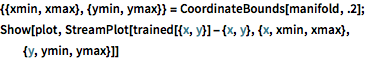
{{xmin, xmax}, {ymin, ymax}} = CoordinateBounds[manifold, .2];
Show[plot,
StreamPlot[
trained[{x, y}] - {x, y}, {x, xmin, xmax}, {y, ymin, ymax}]]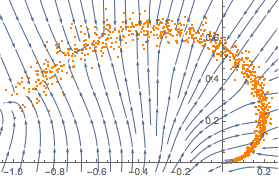
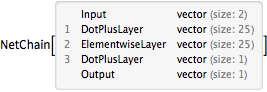
Divida a rede em "codificador" e "decodificador" (o codificador parametriza pontos usando um único valor escalar, enquanto o decodificador reconstrói o ponto a partir desta parametrização).
decoder = Drop[trained, 3]
encoder = Take[trained, 3]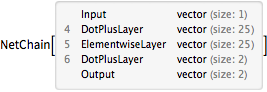
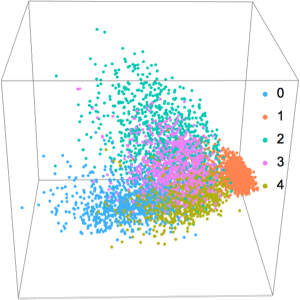
Coloque uma cor para cada ponto na variedade original por sua parametrização sob o codificador.
ListPlot[Style[#, Hue[First[0.3 + encoder[#]]/3]] & /@ manifold]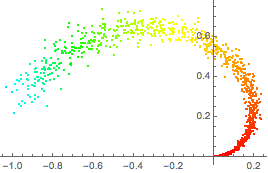
Obtenha a faixa da parametrização aplicando o codificador à variedade.
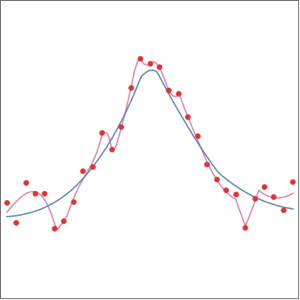
{min, max} = MinMax[encoder[manifold]]Mostre a reconstrução acima desta faixa junto com a variedade original.
Show[plot, ListLinePlot[Table[decoder[x], {x, min, max, .01}]]]