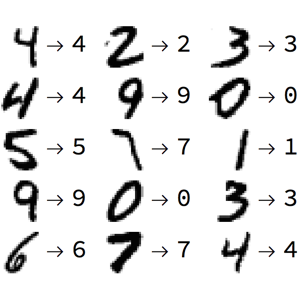Изучение параметризации многообразия
Изучите параметризацию многообразия, к которой относятся входные данные, используя автокодировщик, сеть с узким слоем, изучающим реконструкцию первичного ввода.
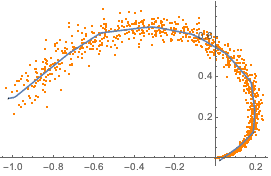
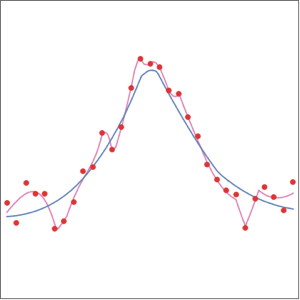
Пример данных режима обучения из части синтезированного двумерного многообразия.

manifold =
Table[AngleVector[{x, 0.9 Pi x}] +
x/20*RandomVariate[NormalDistribution[], 2], {x, 0, 1, 0.001}];
plot = ListPlot[manifold, PlotStyle -> Orange]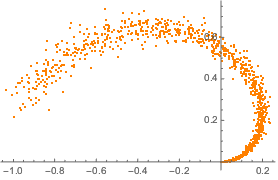
Создайте сеть с узким слоем для изучения параметризации многообразия.
net = NetChain[{25, Ramp, 1, 25, Ramp, 2}, "Input" -> 2]
Создайте сеть потерь, которая рассчитывает потери, основанные на "ошибке восстановления" - измерение степени, до которой сеть может производить выход идентичный вводу.
lossNet =
NetGraph[{net, MeanSquaredLossLayer[]}, {1 -> 2,
NetPort["Input"] -> NetPort[2, "Target"]}]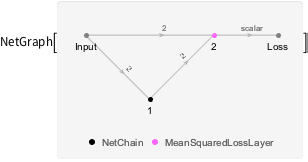
Обучите сеть потерь на многообразии и выявите начальную сеть из сети потерь.
lossNet =
NetTrain[lossNet, <|"Input" -> manifold|>, BatchSize -> 4096];
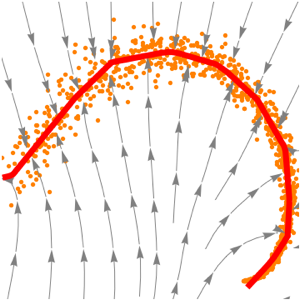
trained = NetExtract[lossNet, 1];Визуализируйте, как сеть проектирует произвольные точки на многообразие.
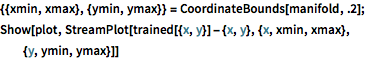
{{xmin, xmax}, {ymin, ymax}} = CoordinateBounds[manifold, .2];
Show[plot,
StreamPlot[
trained[{x, y}] - {x, y}, {x, xmin, xmax}, {y, ymin, ymax}]]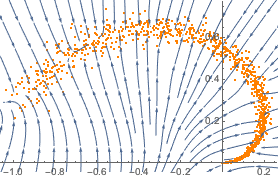
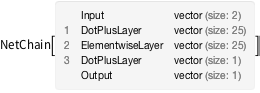
Разделите сеть на сеть кодировщика и декодера (кодировщик параметризует точки, используя одиночную скалярную величину, в то время как декодер восстанавливает точку из параметризации).
decoder = Drop[trained, 3]
encoder = Take[trained, 3]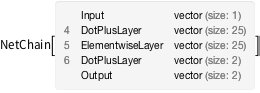
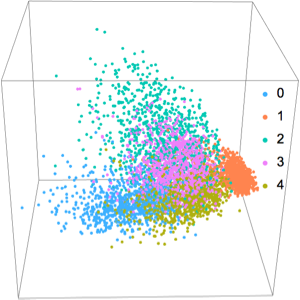
Раскрасьте каждую точку в оригинальном многообразии согласно её параметризации в кодировщике.
ListPlot[Style[#, Hue[First[0.3 + encoder[#]]/3]] & /@ manifold]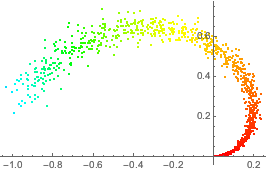
Получите диапазон параметризации путём применения кодировщика к многообразию.
{min, max} = MinMax[encoder[manifold]]Изобразите восстановление в этом диапазоне наряду с оригинальным многообразием.
Show[plot, ListLinePlot[Table[decoder[x], {x, min, max, .01}]]]