Study Dispersion in Quantum Mechanics
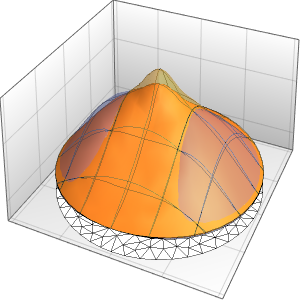
Solve the one-dimensional Schrödinger equation for a free particle that is initially strongly localized around 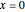 .
.
In[1]:=
eqn = I D[\[Psi][x, t], t] == D[\[Psi][x, t], {x, 2}];
sol[x_, t_] =
DSolveValue[{eqn, \[Psi][x, 0] == Exp[-x^2]}, \[Psi][x, t], {x, t}]Out[1]=
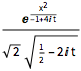
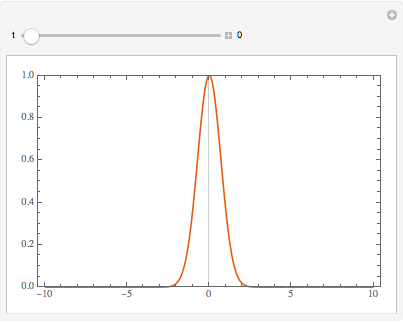
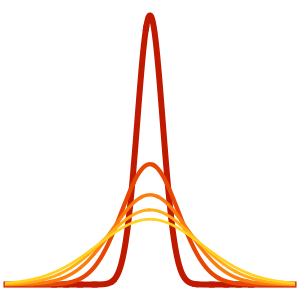
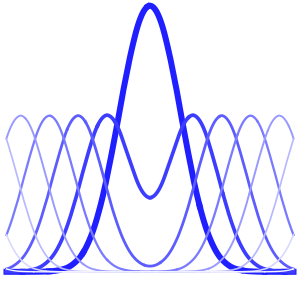
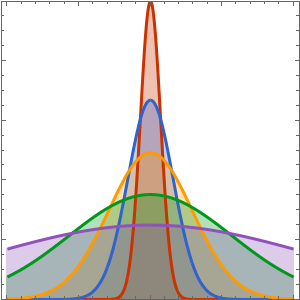
As time increases, the wavefunction becomes less sharply peaked at the origin.
In[2]:=

Manipulate[
Plot[Abs@sol[x, t], {x, -10, 10}, PlotRange -> {0, 1},
PlotTheme -> "Scientific", ImageSize -> Medium], {t, 0, 5,
Appearance -> "Labeled"}]