さまざまな単位を持つランダムなベクトル
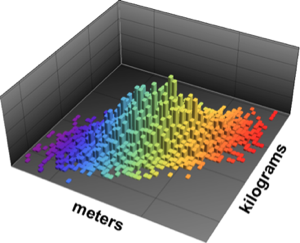
相関係数を0.65と想定して,身長と体重の結合分布を定義する.
In[1]:=
hw\[ScriptCapitalD] =
BinormalDistribution[{Quantity[1.8, "Meters"],
Quantity[85, "Kilograms"]}, {Quantity[0.15, "Meters"],
Quantity[9, "Kilograms"]}, 0.65]Out[1]=
ある人の体重が72キログラムを超える場合に,その人の身長が1.75メートルを超える確率を計算する.
In[2]:=
NProbability[
h > Quantity[1.75, "m"] \[Conditioned]
w > Quantity[72, "kg"], {h, w} \[Distributed] hw\[ScriptCapitalD]]Out[2]=
想定母集団について,肥満度指数(BMI)の分布を計算する.
In[3]:=
bmi\[ScriptCapitalD] =
TransformedDistribution[
w/h^2, {h, w} \[Distributed] hw\[ScriptCapitalD]]Out[3]=
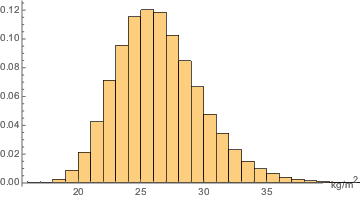
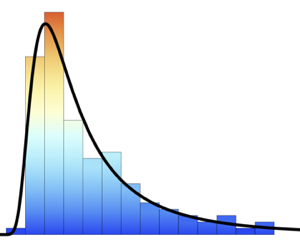
サンプルのヒストグラムを使ってBMIの分布を推定する.
In[4]:=
sample = RandomVariate[bmi\[ScriptCapitalD], 10^5];
Histogram[sample, Automatic, "PDF", AxesLabel -> Automatic]Out[4]=