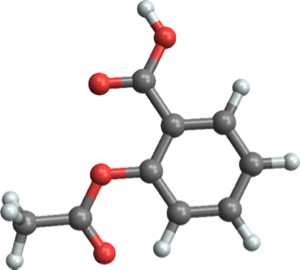
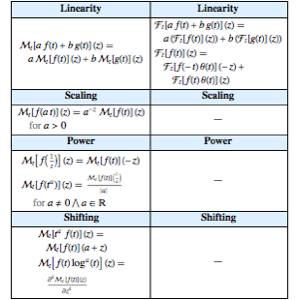
Prepare Aspirin
Aspirin is one of the most commonly used medications for treating pain, fever, and inflammation. It can be synthesized by combining equimolar amounts of salicylic acid and acetic anhydride. Here, chemical data from the Wolfram Knowledgebase is used together with the quantity framework and entity groups, copies, and instances to study the chemical preparation of aspirin.
Represent a typical laboratory batch for a 100-millimolar preparation of aspirin using EntityGroup.

reactants =
EntityGroup[{EntityInstance[Entity["Chemical", "SalicylicAcid"],
Quantity[0.1, "Moles"]],
EntityInstance[Entity["Chemical", "AceticAnhydride"],
Quantity[0.1, "Moles"]]}]Compute the total mass of this batch using a "curried" form of an entity-property query.
mass = reactants["AbsoluteMass"]Because acetic anhydride is a liquid, it would be convenient to know exactly how much is needed.

UnitConvert[
EntityInstance[Entity["Chemical", "AceticAnhydride"],
Quantity[0.1, "Moles"]]["AbsoluteVolume"], "Milliliter"]Assuming a stoichiometric, i.e. a (theoretical) quantitative reaction, this yields 100 millimoles of aspirin. However, in practice, yields of about 90% will be achieved.
EntityInstance[Entity["Chemical", "Aspirin"],
0.9*Quantity[0.1, "Moles"]]["AbsoluteMass"]Count constituent atoms of the aspirin molecule.
elem = Entity["Chemical", "Aspirin"]["ElementCounts"]Assemble the proper numbers of these atoms into a grouped entity expression.
atomAssemble =
EntityGroup[
MapThread[EntityCopies[#1, #2] &, {Keys[elem], Values[elem]}]]atomicmass = atomAssemble["AtomicMass"]As expected, the overall atomic mass of this entity group coincides with the molar mass of the whole molecule.
molarmass =
Entity["Chemical", "Aspirin"][
EntityProperty["Chemical", "MolarMass"]]Equal @@ QuantityMagnitude /@ {atomicmass, molarmass}However, there are other possible isotopic combinations, each of them with a slightly different total mass.
stableIsotopes = #[EntityProperty["Element", "StableIsotopes"]] & /@
Keys[elem]This group consists of the standard isotopes only (the so-called "principal ion").

EntityGroup[{EntityCopies[Entity["Isotope", "C12"], 9],
EntityCopies[Entity["Isotope", "H1"], 8],
EntityCopies[Entity["Isotope", "O16"], 4]}]["AtomicMass"]The probability of the occurrence of a molecule with such a composition is less than 90%. Nevertheless, in a mass spectrum it would be the most prominent molecular peak.

Times @@ MapThread[(QuantityMagnitude[#1[
EntityProperty["Isotope", "IsotopeAbundance"]],
"PureUnities"])^#2 &, {stableIsotopes[[All, 1]], Values[elem]}]