Valuate a Bag of Coins
A bag of new US coins is stolen from a bank. Without opening the bag, what can be said about the monetary value of its contents? One obvious and easily measured physical characteristic is the bag's weight. Assuming a one-pound bag of coins, combine the Wolfram Knowledgebase's know-how on currencies and built-in ability to solve linear equations to study the expected value of the plunder.
To begin, return a list of US coins in current circulation by means of an implicitly defined entity class.

EntityClass["CurrencyDenomination", {EntityProperty[
"CurrencyDenomination", "IssuingCountry"] ->
Entity["Country", "UnitedStates"],
EntityProperty["CurrencyDenomination", "Format"] -> "coin"}]Expand the implicitly defined entity class by clicking the [+], find its members, and sort them by value.

coinsUS = EntityList[
EntityClass[
"CurrencyDenomination", {
EntityProperty[
"CurrencyDenomination", "IssuingCountry"] -> Entity[
"Country", "UnitedStates"],
EntityProperty["CurrencyDenomination", "Format"] -> "coin"}]] //
SortBy[#[EntityProperty["CurrencyDenomination", "Value"]] &]Make a collage of coin images.
ImageCollage[
EntityValue[coinsUS,
EntityProperty["CurrencyDenomination", "Image"]],
Background -> White]
Summarize coin properties in a table.

TextGrid[{ImageResize[#2, 60], #1,
Row[Riffle[#3, Style[" | ", Gray]]]} & @@@
EntityValue[
coinsUS, {EntityProperty["CurrencyDenomination", "Entity"],
EntityProperty["CurrencyDenomination", "Image"],
EntityProperty["CurrencyDenomination", "PeopleOnCurrency"]}],
Alignment -> {Left, Center}, Dividers -> All] // TraditionalForm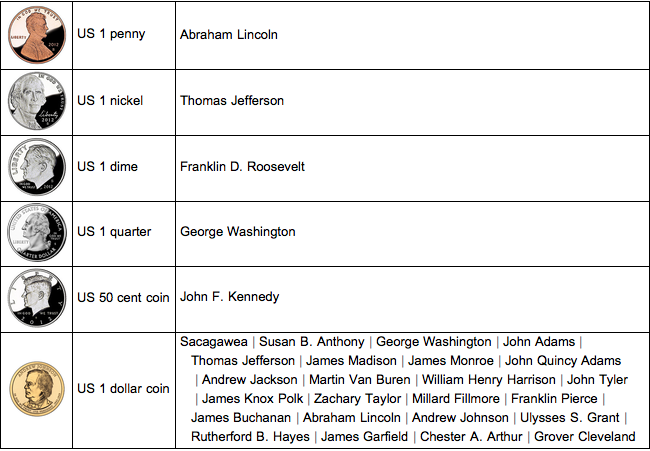
Get coin denominations (in cents) and masses (in grams) and convert masses to rational numbers.
{values, masses} =
Transpose[EntityValue[coinsUS, {"Value", "Weight"}]]
coinsandweights = Transpose[{
QuantityMagnitude[UnitConvert[values, "USCents"]],
Rationalize[QuantityMagnitude[N[UnitConvert[masses, "Grams"]]]]
}]lcm = LCM @@ Denominator[Rationalize[coinsandweights][[All, 2]]];rationalcoinweights = lcm #2 & @@@ Rationalize[coinsandweights]Find all coin distributions that are compatible with a weight measurement of one pound with an error measurement of ± 0.1% (assuming the bag itself contributes negligibly).
meanWeight =
QuantityMagnitude[UnitConvert[Quantity[1, "Pounds"], "Grams"]];error = Normal[Quantity[0.1, "Percent"]];{minScaledWeight,
maxScaledWeight} = {Floor[lcm meanWeight (1 - error/2)],
Ceiling[lcm meanWeight (1 + error/2)]}Use FrobeniusSolve to determine all possible coin collections giving the required total weight.
Flatten[allSolutions, 1] // LengthFind the minimum, median, mean, and maximum values of the total monetary value of the coins in the bag (assuming all combinations are equally likely).
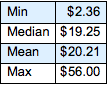
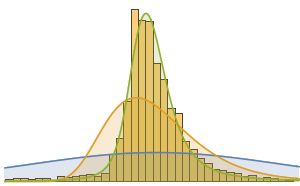
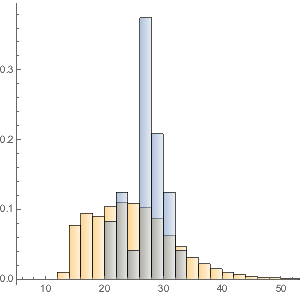
Make a histogram of the distribution of total money value.
Histogram[dollarValues, Automatic, "PDF",
AxesLabel -> {Quantity[None, "USDollars"], "fraction"}]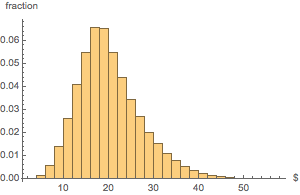
The weight distribution of all sacks is fairly uniform.
Histogram[weightvalues, 50, "PDF",
AxesLabel -> {Quantity[None, "USDollars"], "fraction"}]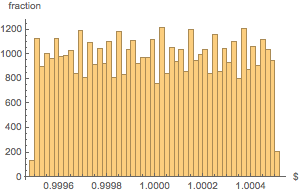
Plot the distribution of the number of coins.
Histogram[Total /@ Flatten[allSolutions, 1], {5}]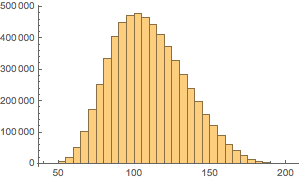
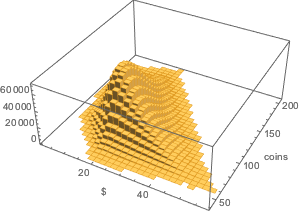
The bivariate distribution of the monetary value versus the number of coins in the sack.
Histogram3D[{coins.#/100., Total[#]} & /@ Flatten[allSolutions, 1],
AxesLabel -> {Quantity[None, "USDollars"], "coins"}]