Encrypt and Store a Treasure Map on the Cloud
Any Wolfram Language expression can be encrypted.
Generate a strong symmetric key derived from a secret password using the Blowfish method.
skeletonKey = GenerateSymmetricKey["Avast ye!", Method -> "Blowfish"]
Encrypt the location of the treasure, stored in a GeoMarker and visualized using GeoGraphics, using the generated key.
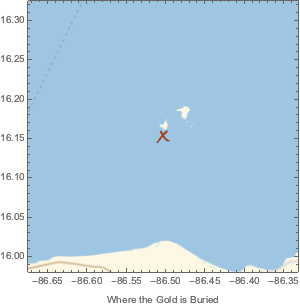
hiddenTreasure = Encrypt[skeletonKey, treasureMap]
Now that the data is safely encrypted using a local key, upload the map to the Wolfram Cloud.
stowed = CloudPut[hiddenTreasure]In order to cover the tracks, discard the original map and key using Clear.
Clear[hiddenTreasure]Clear[skeletonKey]Since the key was derived using a password, you can create a new key using the original input.
newKey = GenerateSymmetricKey["Avast ye!", Method -> "Blowfish"]
The new key can now be used to reference the cloud-deployed map.
reclaimedMap = Decrypt[newKey, CloudGet[stowed]]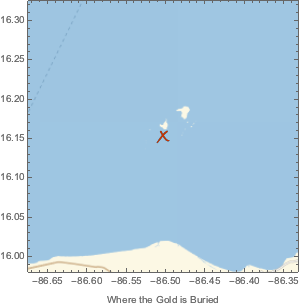
Extract the location of the treasure.
treasureLocation = reclaimedMap[[3, 2]]Ask for driving directions.
TravelDirections[{$GeoLocation, treasureLocation}]As there is no driving route to the treasure, compute its distance using GeoDistance.
GeoDistance[$GeoLocation, treasureLocation]Given the distance, locate the nearest airport to the treasure.
airport = First[GeoNearest["Airport", treasureLocation]]The distance from that airport to the treasure.
GeoDistance[airport, treasureLocation]