Approximate Signal Derivative
Use MovingMap to approximate the derivative of a signal coming from irregularly sampled continuous time series.
In[1]:=
ts = TimeSeries[
Table[{t, EllipticTheta[1, t, 0.3]}, {t,
Join[{0.}, RandomReal[{0, 2 Pi}, 254], {2. Pi}]}]]Out[1]=
In[2]:=
RegularlySampledQ[ts]Out[2]=
In[3]:=
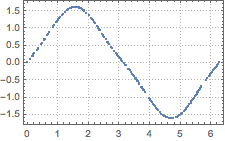
ListPlot[ts, PlotTheme -> "Detailed"]Out[3]=
Use the values and the times at the boundaries of each sliding window to compute the difference quotients.
In[4]:=
quotient[values_, times_] :=
First[Differences[values]/Differences[times]]In[5]:=
mm = MovingMap[quotient[#BoundaryValues, #BoundaryTimes] &,
ts, {.01, Right}]Out[5]=
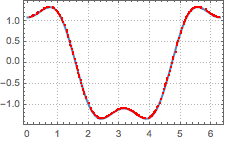
Compare to the theoretical derivative.
In[6]:=
prime = D[EllipticTheta[1, t, 0.3], t]Out[6]=
In[7]:=
Show[Plot[prime, {t, 0, 2 \[Pi]}, PlotStyle -> Thick,
PlotTheme -> "Detailed", PlotLegends -> None],
ListPlot[mm, PlotStyle -> Red]]Out[7]=
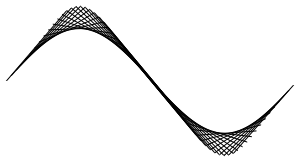
Use MovingMap with Line in place of the quotient function to create a plot of secant lines that approximate the original time series.
In[8]:=
line[yvals_, xvals_] := Line[Transpose[{xvals, yvals}]];In[9]:=
lines = MovingMap[ line[#BoundaryValues, #BoundaryTimes] &,
ts, {1.3, Right, {0, 2. \[Pi], .1}}];In[10]:=
Graphics[{Black, lines["Values"]}]Out[10]=