Manned Space Missions
MannedSpaceMissionData provides historic and current information about human space exploration.
In[1]:=
missions = MannedSpaceMissionData[];You can create an EventSeries based on the launch date of the missions with vector values storing the mission entity and the duration of each mission.
In[2]:=
data = DeleteMissing[
MannedSpaceMissionData[
missions, {"LaunchDate", "Entity", "MissionDuration"}], 1, 2];In[3]:=
es = EventSeries[data[[All, {2, 3}]], {data[[All, 1]]}]Out[3]=
TimelinePlot of the time stamps shows the almost-continuous span of manned spaced missions since 1961.
In[4]:=
TimelinePlot[es["Dates"]]Out[4]=
To analyze the missions' durations, extract the second component of the original event series and convert the values to hours.
In[5]:=
durations = UnitConvert[es["PathComponent", 2], "Hours"]Out[5]=
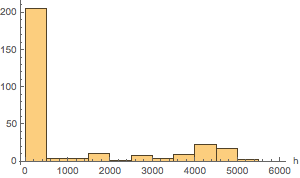
The short missions are most common.
In[6]:=
Histogram[durations, Quantity[{0, 6000, 500}, "Hours"],
AxesLabel -> Automatic]Out[6]=
show complete Wolfram Language input
In[8]:=
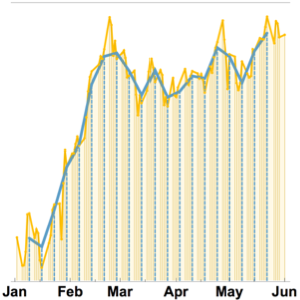
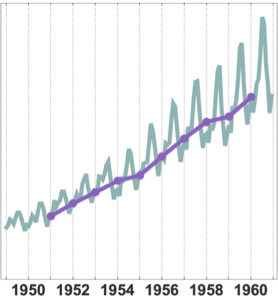
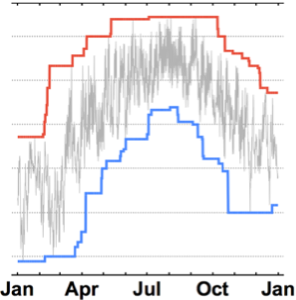
DateListPlot[{durations, line1, line2}, opts]Out[8]=
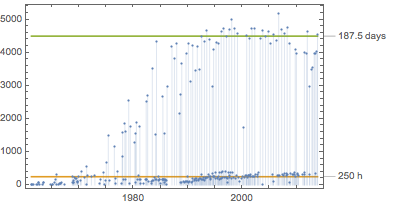
Compute some descriptive statistics of the mission durations. Note the mean and the median being far apart, indicating a long tail distribution.
In[9]:=

stats = {Min, Max, Mean, Median};
convert :=
UnitConvert[N[#], MixedUnit[{"Months", "Days", "Hours", "Minutes"}]]
&In[10]:=
TableForm[Map[convert[#[durations]] &, stats],
TableHeadings -> {stats}]Out[10]//TableForm=

The total time that there was a human in space.
In[11]:=
UnitConvert[Total[durations],
MixedUnit[{"Years", "Months", "Days", "Hours", "Minutes",
"Seconds"}]]Out[11]=